题目内容
已知向量 与
与 的夹角为120°,且|
的夹角为120°,且| |=3,|
|=3,| |=2.若
|=2.若 =λ
=λ +
+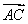 ,且
,且 ⊥
⊥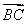 ,则实数λ的值为________.
,则实数λ的值为________.
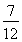
【解析】∵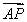 ⊥
⊥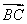 ,∴
,∴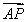 ·
·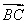 =
=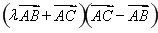 =-λ
=-λ 2+
2+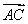 2+
2+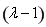
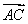 ·
·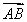 =0,
=0,
即-λ×9+4+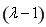 ×3×2×
×3×2×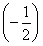 =0,解得λ=
=0,解得λ=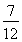 .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
题目内容
已知向量 与
与 的夹角为120°,且|
的夹角为120°,且| |=3,|
|=3,| |=2.若
|=2.若 =λ
=λ +
+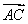 ,且
,且 ⊥
⊥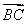 ,则实数λ的值为________.
,则实数λ的值为________.
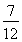
【解析】∵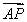 ⊥
⊥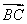 ,∴
,∴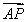 ·
·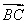 =
=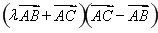 =-λ
=-λ 2+
2+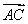 2+
2+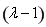
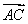 ·
·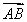 =0,
=0,
即-λ×9+4+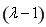 ×3×2×
×3×2×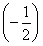 =0,解得λ=
=0,解得λ=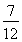 .
.

 备战中考寒假系列答案
备战中考寒假系列答案