题目内容
某学生社团在对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排共有两种:白天背和晚上睡前背。为了研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样,并完成一项实验.实验方法是,使两组学生记忆40个无意义音节(如XIQ、GEH),均要求在刚能全部记清时就停止识记,并在8小时后进行记忆检测。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验.
两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点而不含右端点).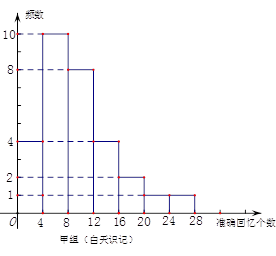
(1)估计这1000名被调查学生中停止后8小时40个音节的保持率不小于60%的人数;
(2)从乙组准确回忆单词个数在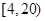 个范围内的学生中随机选2人,求能准确回忆
个范围内的学生中随机选2人,求能准确回忆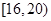 个单词至少有一人的概率.
个单词至少有一人的概率.
(Ⅰ)180人;(Ⅱ)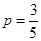 .
.
解析试题分析:首先弄清题意,1000名学生分为了两类,每类学生有多少人?先求出抽取的样本中的个体数,然后再根据图形求甲组中的个体数,从而可得乙组中的个体数。从乙组的频率分布直方图可得各段的频率,然后可得各段的人数。弄清以上数据,便可解决该题。
试题解析:总共抽取了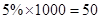 人,由甲组的条形图可知甲组有有:4+10+8+4+2+1+1=30人;故乙组有20人
人,由甲组的条形图可知甲组有有:4+10+8+4+2+1+1=30人;故乙组有20人
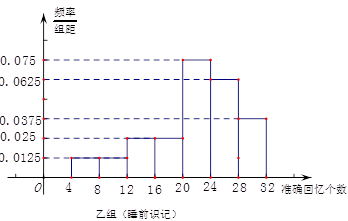
乙组的频率为: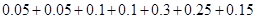 即有1+1+2+2+6+5+3=20人。
即有1+1+2+2+6+5+3=20人。
因为按5%的比例对这1000名学生按时间安排类型进行分层抽样
所以“白天背”的同学共有 人,“晚上睡前背”的同学有400人。
人,“晚上睡前背”的同学有400人。
(Ⅰ)40个音节的保持率不小于60%,则至少能准确回忆24个,
“白天背”的同学共有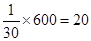 人,“晚上睡前背”的同学有
人,“晚上睡前背”的同学有 人。
人。
所以这1000名被调查学生中停止后8小时40个音节的保持率不小于60%的人数大约为180人
(Ⅱ)乙组准确回忆单词个数在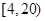 个范围内的学生有6人,能准确回忆
个范围内的学生有6人,能准确回忆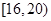 个单词的学生有2人。
个单词的学生有2人。
从6人中随机抽取2人,用列举法可得有15种可能结果
法一、两人都能准确回忆 个单词的可能结果有6种,故所求概率为:
个单词的可能结果有6种,故所求概率为:
法二、至少有一人能准确回忆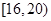 个单词的可能结果有
个单词的可能结果有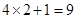 种,故所求概率为:
种,故所求概率为: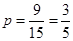
考点:抽样方法,条形图,频率分布直方图及古典概型的计算

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(2)若线性相关,则求出回归方程
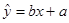 ;
;(3)估计使用年限为10年时,维修费用是多少?
(参考公式:
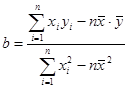 ,
, )
) 为预防H7N9病毒爆发,某生物技术公司研制出一种H7N9病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 | A组 | B组 | C组 |
| 疫苗有效 | 673 | 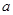 | 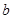 |
| 疫苗无效 | 77 | 90 | 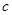 |
(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在C组抽取样本多少个?
(2)已知
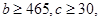 求通过测试的概率.
求通过测试的概率. (本小题满分12分)
某学校高二年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(1)完成下面的 列联表;
列联表;
| | 不喜欢运动 | 喜欢运动 | 合计 |
| 女生 | 50 | | |
| 男生 | | | |
| 合计 | | 100 | 200 |
 和
和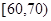 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.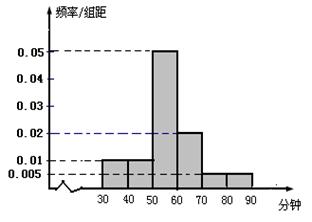
天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的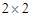 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为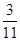 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:
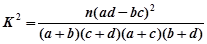 。
。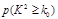 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
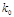 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
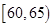 ,
, ,
, ,
, ,
, ,
, 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 的分布列及其数学期望。(12分)
的分布列及其数学期望。(12分)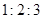 ,其中第二小组的频数为12.
,其中第二小组的频数为12.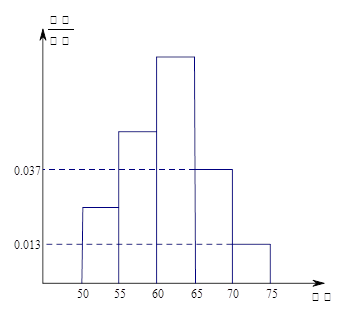
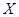 表示体重超过60公斤的学生人数,求
表示体重超过60公斤的学生人数,求 表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
 及这6位同学成绩的标准差s;
及这6位同学成绩的标准差s; 与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为 )作为样本如下表所示.
)作为样本如下表所示.
 ;
; ,试估计此人的身高;
,试估计此人的身高; ,
, ,
, ,
, )
)