题目内容
设a,b,c∈R+,若( a+b+c ) ( +
+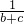 )≥k恒成立,则k的最大值是________.
)≥k恒成立,则k的最大值是________.
4
分析:将( a+b+c ) ( +
+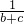 )展开,利用基本不等式求出其最小值,即得k的最大值.
)展开,利用基本不等式求出其最小值,即得k的最大值.
解答:a,b,c∈R+,
∵( a+b+c ) ( +
+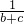 )=2+
)=2+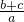 +
+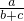 ≥2+2
≥2+2 =4,等号当且仅当
=4,等号当且仅当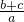 =
=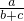 时成立
时成立
又a,b,c∈R+,若( a+b+c ) ( +
+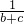 )≥k恒成立,
)≥k恒成立,
∴k≤4
故答案为4
点评:本题考查基本不等式在最值问题中的应用,解题的关键是对不等式左边进行恒等变形构造出积为定值的形式,利用基本不等式求出左侧的最小值,根据恒成立的关系得到参数的最大值
分析:将( a+b+c ) (
 +
+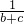 )展开,利用基本不等式求出其最小值,即得k的最大值.
)展开,利用基本不等式求出其最小值,即得k的最大值.解答:a,b,c∈R+,
∵( a+b+c ) (
 +
+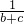 )=2+
)=2+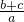 +
+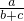 ≥2+2
≥2+2 =4,等号当且仅当
=4,等号当且仅当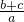 =
=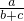 时成立
时成立又a,b,c∈R+,若( a+b+c ) (
 +
+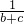 )≥k恒成立,
)≥k恒成立,∴k≤4
故答案为4
点评:本题考查基本不等式在最值问题中的应用,解题的关键是对不等式左边进行恒等变形构造出积为定值的形式,利用基本不等式求出左侧的最小值,根据恒成立的关系得到参数的最大值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目