题目内容
在正三棱锥P-ABC中，D为PA的中点，O为△ABC的中心，给出下列四个结论：①OD∥平面PBC； ②OD⊥PA；③OD⊥BC； ④PA=2OD．其中正确结论的序号是
③④
③④
．分析：取BC中点M，连接AM，PM，则O∈AM．由AO=2OM，OD与PM不平行，故OD不平行于平面PBC；由OA≠OP，D为PA中点，知OD与PA不垂直；同P-ABC为正三棱锥，知BC⊥PM，BC⊥AM，所以OD⊥BC；由PO垂直于平面ABC，OA属于平面ABC，知PO垂直于OA，△AOP为直角三角形，所以PA=2OD．
解答：解：取BC中点M，连接AM，PM，
则O∈AM．
∵AO=2OM，
∴OD与PM不平行，
∴OD∥平面PBC不成立，即①错误；
∵OA≠OP，D为PA中点，
∴OD⊥PA不成立，即②错误；
∵P-ABC为正三棱锥，
∴BC⊥PM，BC⊥AM，
∴BC⊥面APM，
∴OD⊥BC，即③成立；
∵PO垂直于平面ABC，OA属于平面ABC
∴PO垂直于OA
∴三角形AOP为直角三角形
∵D为AP中点
∴PA=2OD，即④成立．
故答案为：③④．
则O∈AM．
∵AO=2OM，
∴OD与PM不平行，
∴OD∥平面PBC不成立，即①错误；
∵OA≠OP，D为PA中点，
∴OD⊥PA不成立，即②错误；
∵P-ABC为正三棱锥，
∴BC⊥PM，BC⊥AM，
∴BC⊥面APM，
∴OD⊥BC，即③成立；
∵PO垂直于平面ABC，OA属于平面ABC
∴PO垂直于OA
∴三角形AOP为直角三角形
∵D为AP中点
∴PA=2OD，即④成立．
故答案为：③④．
点评：本题考查棱锥的结构特征，解题时要认真审题，仔细解答，注意观察，熟练掌握棱锥的性质．
练习册系列答案
相关题目
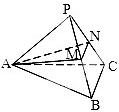如图，在正三棱锥P-ABC中，M、N分别是侧棱PB、PC的中点，若截面AMN⊥侧面PBC，底面边长为2，则此三棱锥的体积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|