题目内容
已知点M(2,0),P为抛物线C:y2=2px(p>0)上一动点,若|PM|的最小值为
.
(1)求抛物线C的方程;
(2)已知⊙M:(x-2)2+y2=r2(r>0),过原点O作⊙M的两条切线交抛物线于A,B两点,若直线AB与⊙M也相切.
(i)求r的值;
(ii)对于点Q(t2,t),抛物线C上总存在两个点R,S,使得△QRS三边与⊙M均相切,求t的取值范围.
| ||
| 2 |
(1)求抛物线C的方程;
(2)已知⊙M:(x-2)2+y2=r2(r>0),过原点O作⊙M的两条切线交抛物线于A,B两点,若直线AB与⊙M也相切.
(i)求r的值;
(ii)对于点Q(t2,t),抛物线C上总存在两个点R,S,使得△QRS三边与⊙M均相切,求t的取值范围.
分析:(1)点M(2,0),P为抛物线C:y2=2px(p>0)上一动点,设P(
,y),所以|PM|2=(
-2)2+y2=
y4+(1-
)y2+4,由此能求出抛物线C的方程.
(2)(i)由题意A(2+r,
),B(2+r,-
),知kOA=
,由此能求出r.
(ii)设R(t12,t1),S(t22,t2)(t1≠t2),则QR:y=
x+
,△QRS三边与⊙M均相切,故
=1,由此能求出t.
| y2 |
| 2p |
| y2 |
| 2p |
| 1 |
| 4p2 |
| 2 |
| p |
(2)(i)由题意A(2+r,
| 2+r |
| 2+r |
| 1 | ||
|
(ii)设R(t12,t1),S(t22,t2)(t1≠t2),则QR:y=
| 1 |
| t+t1 |
| tt1 |
| t+t1 |
| |2+tt1| | ||
|
解答:解:(1)∵点M(2,0),P为抛物线C:y2=2px(p>0)上一动点,设P(
,y),
∴|PM|2=(
-2)2+y2=
y4+(1-
)y2+4,
∴对称轴为y2=2p(2-p).
当p≥2,|PM|min=2,舍
当0<p<2,|PM|min=4p-p2=
,解得p=
或
(舍),
所以y2=x.
(2)(i)由题意A(2+r,
),B(2+r,-
),
∴kOA=
,
OA:y=
x,∴
=r,
∴(r-1)(r+2)2=1,
解得r=1.
(ii)设R(t12,t1),S(t22,t2)(t1≠t2),则QR:y=
x+
∵△QRS三边与⊙M均相切,
∴
=1,从而t12(1-t2)-2tt1+t2-3=0,将t1换成t2也成立
因为t1≠t2,所以t2≠1
故t1,t2为方程(1-t2)x2-2tx+t2-3=0的两根,
∴t1+t2=
,t1t2=
,
故RS:y=
x+
,即y=
x+
,
圆心到RS的距离
=1,
解得t=±1.
故t的取值范围是{-1,1}.
| y2 |
| 2p |
∴|PM|2=(
| y2 |
| 2p |
| 1 |
| 4p2 |
| 2 |
| p |
∴对称轴为y2=2p(2-p).
当p≥2,|PM|min=2,舍
当0<p<2,|PM|min=4p-p2=
| 7 |
| 4 |
| 1 |
| 2 |
| 7 |
| 2 |
所以y2=x.
(2)(i)由题意A(2+r,
| 2+r |
| 2+r |
∴kOA=
| 1 | ||
|
OA:y=
| 1 | ||
|
| 2 | ||
|
∴(r-1)(r+2)2=1,
解得r=1.
(ii)设R(t12,t1),S(t22,t2)(t1≠t2),则QR:y=
| 1 |
| t+t1 |
| tt1 |
| t+t1 |
∵△QRS三边与⊙M均相切,
∴
| |2+tt1| | ||
|
因为t1≠t2,所以t2≠1
故t1,t2为方程(1-t2)x2-2tx+t2-3=0的两根,
∴t1+t2=
| 2t |
| 1-t2 |
| t2-3 |
| 1-t2 |
故RS:y=
| 1 |
| t1+t2 |
| t1t2 |
| t1+t2 |
| 1-t2 |
| 2t |
| t2-3 |
| 2t |
圆心到RS的距离
| |2(1-t2)+t2-3| | ||
|
解得t=±1.
故t的取值范围是{-1,1}.
点评:本题考查抛物线方程的求法,考查实数值的求法,考查满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意点到直线的距离公式的求法.

练习册系列答案
相关题目
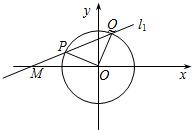 已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的
已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的