题目内容
已知点M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2
.记动点P的轨迹为W.
(1)求W的方程;
(2)若A,B是W上的不同两点,O是坐标原点,求
•
的最小值.
| 2 |
(1)求W的方程;
(2)若A,B是W上的不同两点,O是坐标原点,求
| OA |
| OB |
分析:(1)利用双曲线的定义,可求W的方程;
(2)设点的坐标,利用向量的数量积公式,结合基本不等式,可求
•
的最小值.
(2)设点的坐标,利用向量的数量积公式,结合基本不等式,可求
| OA |
| OB |
解答:解:(1)据题意M(-2,0),N(2,0),动点P满足条件|PM|-|PN|=2
,
∴|PM|-|PN|=2
<4
∴动点P的轨迹为双曲线的右支,且c=2,a=
,
∴曲线方程为x2-y2=2(x≥
);
(2)设A(x1,y1)、B(x2,y2),x1≥
,x2≥
,则x1x2≥2
∴
•
=x1x2+y1y2≥x1x2-
×
≥
=x1x2-|x1x2-2|
=x1x2-(x1x2-2)=2
∴
•
的最小值是2.
| 2 |
∴|PM|-|PN|=2
| 2 |
∴动点P的轨迹为双曲线的右支,且c=2,a=
| 2 |
∴曲线方程为x2-y2=2(x≥
| 2 |
(2)设A(x1,y1)、B(x2,y2),x1≥
| 2 |
| 2 |
∴
| OA |
| OB |
| x12-2 |
| x22-2 |
| (x1x2-2)2 |
=x1x2-(x1x2-2)=2
∴
| OA |
| OB |
点评:本题考查轨迹方程,考查双曲线的定义,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
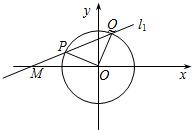 已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的
已知点M(-2,0),⊙O:x2+y2=1(如图);若过点M的直线l1交圆于P、Q两点,且圆孤PQ恰为圆周的