Question

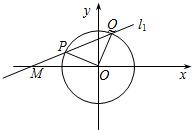已知点M（-2，0），⊙O：x²+y²=1（如图）；若过点M的直线l₁交圆于P、Q两点，且圆孤PQ恰为圆周的

1

4

，求直线l₁的方程．

Answer 1

分析：通过圆孤PQ恰为圆周的

1

4

，求出∠POQ，再求出O点到直线l₁的距离，设出直线l₁的方程，利用点到直线的距离公式，求出变量，即可得到所求直线l₁的方程．

解答：解：∵PQ为圆周的

1

4

，∴∠POQ=

π

2

.
∴O点到直线l₁的距离为

2

2

.
设l₁的方程为y=k(x+2)，∴

|2k|

k2+1

=

2

2

，∴k2=

1

7

.
∴l₁的方程为y=±

7

7

(x+2).

点评：本题是基础题，考查点到直线的距离的应用，待定系数法的解题思想，常考题，一般情况下是选择题或填空题的形式出现．