题目内容
已知函数
(Ⅰ)当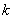 =2时,求曲线
=2时,求曲线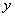 =
=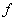 (
(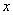 )在点(1,
)在点(1,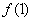 )处的切线方程;
)处的切线方程;
(Ⅱ)求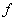 (
(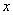 )的单调区间。
)的单调区间。
【答案】
解:(I)当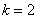 时,
时,
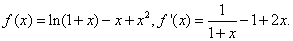
由于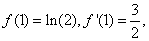 所以曲线
所以曲线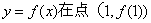 处的切线方程为
处的切线方程为
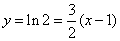 。即
。即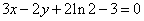
(II)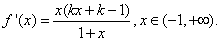
当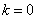 时,
时,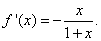
因此在区间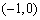 上,
上,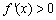 ;在区间
;在区间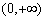 上,
上,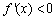 ;
;
所以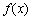 的单调递增区间为
的单调递增区间为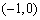 ,单调递减区间为
,单调递减区间为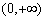 ;
;
当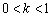 时,
时,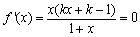 ,得
,得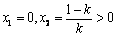 ;
;
因此,在区间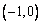 和
和 上,
上,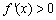 ;在区间
;在区间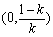 上,
上,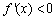 ;
;
即函数 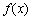 的单调递增区间为
的单调递增区间为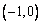 和
和 ,单调递减区间为
,单调递减区间为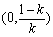 ;
;
当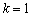 时,
时,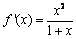 .
.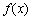 的递增区间为
的递增区间为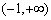
当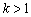 时,由
时,由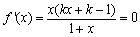 ,得
,得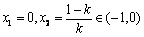 ;
;
因此,在区间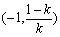 和
和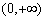 上,
上,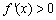 ,在区间
,在区间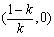 上,
上,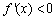 ;
;
即函数 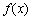 的单调递增区间为
的单调递增区间为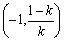 和
和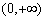 ,单调递减区间为
,单调递减区间为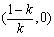 。
。

练习册系列答案
相关题目
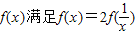 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间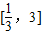 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )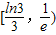
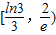
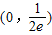
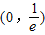
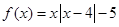 ,则当方程
,则当方程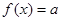 有三个不同实根时,实数
有三个不同实根时,实数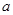 的取值范围
是 ( )
的取值范围
是 ( ) B.
B.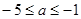 C.
C.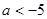 D.
D.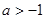
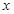 )=
)= ,当
,当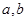 的值及函数f(
的值及函数f(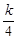 f(
f( ,问
,问 ,当点 (x,y)
是函数y = f (x) 图象上的点时,点
,当点 (x,y)
是函数y = f (x) 图象上的点时,点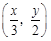 是函数y =
g(x) 图象上的点.
是函数y =
g(x) 图象上的点.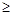 0时,求x的取值范围;
0时,求x的取值范围;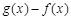 的最大值.
的最大值.