题目内容
已知函数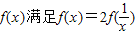 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间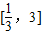 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )A.
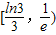
B.
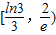
C.
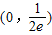
D.
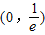
【答案】分析:可以根据函数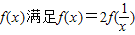 ,求出x在[
,求出x在[ ,1]上的解析式,已知在区间
,1]上的解析式,已知在区间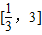 内,函数g(x)=f(x)-ax,有三个不同的零点,对g(x)进行求导,利用导数研究其单调性,从而求出a的范围;
内,函数g(x)=f(x)-ax,有三个不同的零点,对g(x)进行求导,利用导数研究其单调性,从而求出a的范围;
解答:解:在区间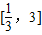 内,函数g(x)=f(x)-ax,有三个不同的零点,
内,函数g(x)=f(x)-ax,有三个不同的零点,
①a>0若x∈[1,3]时,f(x)=lnx,可得g(x)=lnx-ax,(x>0)
g′(x)=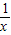 -a=
-a=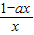 ,
,
若g′(x)<0,可得x>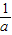 ,g(x)为减函数,
,g(x)为减函数,
若g′(x)>0,可得x<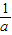 ,g(x)为增函数,
,g(x)为增函数,
此时f(x)必须在[1,3]上有两个交点,
∴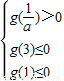 ,解得,
,解得,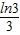 ≤a<
≤a<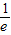 ①
①
设 <x<1,可得1<
<x<1,可得1<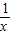 <3,
<3,
∴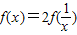 =2ln
=2ln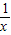 ,此时g(x)=-2lnx-ax,
,此时g(x)=-2lnx-ax,
g′(x)= ,
,
若g′(x)>0,可得x<-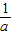 <0,g(x)为增函数
<0,g(x)为增函数
若g′(x)<0,可得x>- ,g(x)为减函数,
,g(x)为减函数,
在[ ,1]上有一个交点,则
,1]上有一个交点,则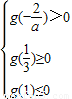 ,解得0<a≤6ln3②
,解得0<a≤6ln3②
综上①②可得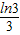 ≤a<
≤a<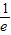 ;
;
②若a<0,对于x∈[1,3]时,g(x)=lnx-ax>0,没有零点,不满足在区间 内,函数g(x)=f(x)-ax,有三个不同的零点,
内,函数g(x)=f(x)-ax,有三个不同的零点,
综上: ≤a<
≤a<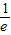 ;
;
故选A;
点评:此题充分利用了分类讨论的思想,是一道综合题,难度比较大,需要排除a<0时的情况,注意解方程的计算量比较大,注意学会如何分类讨论;
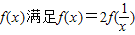 ,求出x在[
,求出x在[ ,1]上的解析式,已知在区间
,1]上的解析式,已知在区间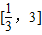 内,函数g(x)=f(x)-ax,有三个不同的零点,对g(x)进行求导,利用导数研究其单调性,从而求出a的范围;
内,函数g(x)=f(x)-ax,有三个不同的零点,对g(x)进行求导,利用导数研究其单调性,从而求出a的范围;解答:解:在区间
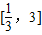 内,函数g(x)=f(x)-ax,有三个不同的零点,
内,函数g(x)=f(x)-ax,有三个不同的零点,①a>0若x∈[1,3]时,f(x)=lnx,可得g(x)=lnx-ax,(x>0)
g′(x)=
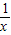 -a=
-a=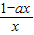 ,
,若g′(x)<0,可得x>
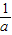 ,g(x)为减函数,
,g(x)为减函数,若g′(x)>0,可得x<
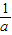 ,g(x)为增函数,
,g(x)为增函数,此时f(x)必须在[1,3]上有两个交点,
∴
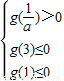 ,解得,
,解得,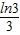 ≤a<
≤a<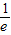 ①
①设
 <x<1,可得1<
<x<1,可得1<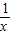 <3,
<3,∴
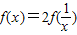 =2ln
=2ln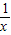 ,此时g(x)=-2lnx-ax,
,此时g(x)=-2lnx-ax,g′(x)=
 ,
,若g′(x)>0,可得x<-
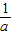 <0,g(x)为增函数
<0,g(x)为增函数若g′(x)<0,可得x>-
 ,g(x)为减函数,
,g(x)为减函数,在[
 ,1]上有一个交点,则
,1]上有一个交点,则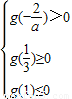 ,解得0<a≤6ln3②
,解得0<a≤6ln3②综上①②可得
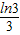 ≤a<
≤a<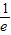 ;
;②若a<0,对于x∈[1,3]时,g(x)=lnx-ax>0,没有零点,不满足在区间
 内,函数g(x)=f(x)-ax,有三个不同的零点,
内,函数g(x)=f(x)-ax,有三个不同的零点,综上:
 ≤a<
≤a<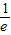 ;
;故选A;
点评:此题充分利用了分类讨论的思想,是一道综合题,难度比较大,需要排除a<0时的情况,注意解方程的计算量比较大,注意学会如何分类讨论;

练习册系列答案
相关题目
已知函数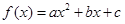 ,当x=1时有最大值1。当
,当x=1时有最大值1。当 时,函数
时,函数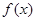 的值域为
的值域为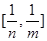 ,则
,则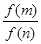 的值为
的值为
A.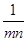 | B.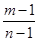 | C.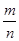 | D.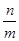 |
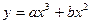 ,当x=
,当x= 1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。
1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。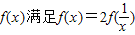 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间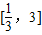 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )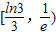
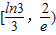
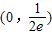
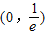
 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )


