题目内容
已知函数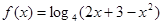 ,(1)求函数的定义域;(2)求
,(1)求函数的定义域;(2)求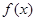 的单调区间;
的单调区间;
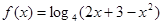 ,(1)求函数的定义域;(2)求
,(1)求函数的定义域;(2)求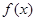 的单调区间;
的单调区间;(1)(-1,3);(2)在(-1,1)上递增,在(1,3)上递减
本试题主要考查了函数的定义域以及函数单调区间的求解运用。
解:(1)由2x+3-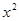 >0得
>0得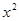 -2x-3<0即(x-3)(x+1)<0所以-1<x<3
-2x-3<0即(x-3)(x+1)<0所以-1<x<3
故函数的定义域为(-1,3) 6分
(2)设u=2x+3-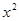 =-(x-1)
=-(x-1)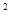 +4 即抛物线的对称轴是x="1" ,开口向下
+4 即抛物线的对称轴是x="1" ,开口向下
则f(x)=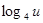
因为函数u在(-1,1)上递增,在(1,3)上递减
又f(x)=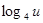 在u
在u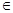 (0,+∞)上是增函数,由复合函数的单调性知:
(0,+∞)上是增函数,由复合函数的单调性知:
f(x)=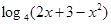 在(-1,1)上递增,在(1,3)上递减 ………………12分
在(-1,1)上递增,在(1,3)上递减 ………………12分
解:(1)由2x+3-
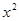 >0得
>0得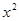 -2x-3<0即(x-3)(x+1)<0所以-1<x<3
-2x-3<0即(x-3)(x+1)<0所以-1<x<3故函数的定义域为(-1,3) 6分
(2)设u=2x+3-
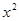 =-(x-1)
=-(x-1)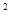 +4 即抛物线的对称轴是x="1" ,开口向下
+4 即抛物线的对称轴是x="1" ,开口向下则f(x)=
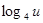
因为函数u在(-1,1)上递增,在(1,3)上递减
又f(x)=
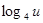 在u
在u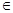 (0,+∞)上是增函数,由复合函数的单调性知:
(0,+∞)上是增函数,由复合函数的单调性知:f(x)=
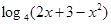 在(-1,1)上递增,在(1,3)上递减 ………………12分
在(-1,1)上递增,在(1,3)上递减 ………………12分
练习册系列答案
相关题目
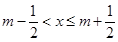 (其中
(其中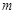 为整数),则
为整数),则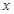 最近的整数,记作
最近的整数,记作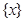 ,
,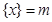 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数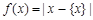 的四个命题:
的四个命题: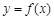 的定义域是R,值域是[0,
的定义域是R,值域是[0,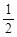 ];
];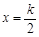 (k∈Z)对称;
(k∈Z)对称;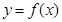 在
在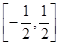 上是增函数;
上是增函数; 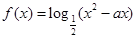 在区间(1,2)内是减函数,则实数a的取值范围是__________.
在区间(1,2)内是减函数,则实数a的取值范围是__________.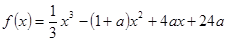 ,其中常数
,其中常数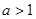
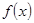 的单调性
的单调性 时,
时,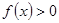 恒成立,求
恒成立,求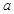 的取值范围
的取值范围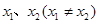 是函数
是函数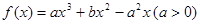 的两个极值点。
的两个极值点。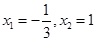 ,求函数
,求函数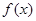 的解析式;
的解析式;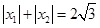 ,求
,求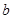 的最大值。
的最大值。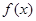 =3
=3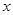 -4
-4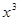 ,
,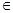 [0,1]的最大值是
[0,1]的最大值是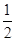
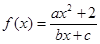 是奇函数,且其图象经过点(1,3)和(2,3)。
是奇函数,且其图象经过点(1,3)和(2,3)。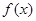 的表达式;
的表达式;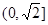 上是减函数;
上是减函数;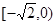 上是增函数还是减函数?(只需写出结论,不需证明)
上是增函数还是减函数?(只需写出结论,不需证明)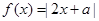 的单调递增区间是
的单调递增区间是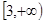 ,则
,则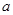 =________.
=________.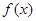 为偶函数,它在
为偶函数,它在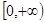 上减函数,若
上减函数,若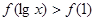 ,则x的取值范围是( )
,则x的取值范围是( )