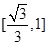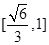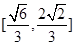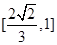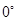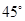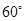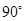题目内容
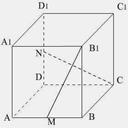
如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )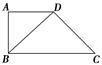
| A.平面ABD⊥平面ABC | B.平面ADC⊥平面BDC |
| C.平面ABC⊥平面BDC | D.平面ADC⊥平面ABC |
D
解析

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则能得出
是两个不同的平面,则能得出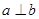 的是( )
的是( )
A.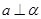 , ,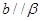 , ,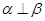 | B.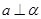 , ,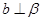 , ,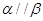 |
C.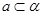 , ,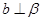 , ,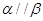 | D.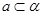 , ,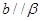 , ,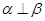 |
设 是不同的直线,
是不同的直线,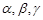 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①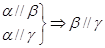 ②
②
③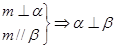 ④
④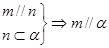
其中,真命题是( )
| A.①④ | B.②③ | C.①③ | D.②④ |
已知m、n为两条不同的直线,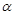 、
、 为两个不同的平面,下列命题中正确的是 ( )
为两个不同的平面,下列命题中正确的是 ( )
A.若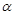 ∥ ∥ ,m∥ ,m∥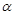 ,则m∥ ,则m∥ | B.若m⊥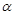 ,m⊥ ,m⊥ ,则 ,则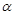 ∥ ∥ |
C.若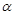 ⊥ ⊥ ,m⊥ ,m⊥ ,则m⊥ ,则m⊥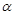 | D.若m∥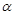 ,m⊥n,则n⊥ ,m⊥n,则n⊥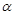 |
设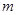 、
、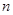 是两条不同的直线,
是两条不同的直线,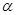 、
、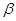 是两个不同的平面,则( )
是两个不同的平面,则( )
A.若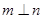 , ,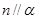 ,则 ,则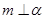 |
B.若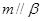 , ,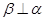 ,则 ,则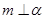 |
C.若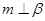 , ,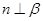 , ,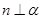 ,则 ,则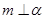 |
D.若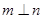 , ,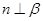 , ,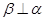 ,则 ,则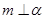 |
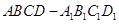 中,点
中,点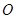 为线段
为线段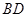 的中点.设点
的中点.设点 在线段
在线段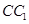 上,直线
上,直线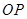 与平面
与平面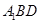 所成的角为
所成的角为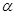 ,则
,则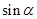 的取值范围是( )
的取值范围是( )