题目内容
3.已知i是虚数单位,则|$\frac{3-i}{(1+i)^{2}}$+$\frac{1+3i}{(1-i)^{2}}$|=$\sqrt{5}$.分析 利用复数的运算法则、模的计算公式即可得出.
解答 解:|$\frac{3-i}{(1+i)^{2}}$+$\frac{1+3i}{(1-i)^{2}}$|=|$\frac{3-i}{2i}$-$\frac{1+3i}{2i}$|=|-2-i|=$\sqrt{5}$.
点评 本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
13.若函数f(x)=3|x-2|-m-2有唯一的零点,则直线mx+ky+3k-2=0恒过定点为( )
| A. | ($\frac{2}{7},-3$) | B. | (-2,-3) | C. | (0,$\frac{2}{7}$) | D. | (-2,0) |
14.已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),且f(1)=2,则f(2015)的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | -1 |
18.已知复数z满足z=$\frac{(1+i)(2-i)}{i}$(i为虚数单位),则$\overline{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.下列说法中正确的序号为( )
| A. | 若直线l平行于平面α内的无数条直线,则l∥α; | |
| B. | 若α∥β,a?α,b?β,则a与b是异面直线; | |
| C. | 若α∥β,a?α,则a∥β; | |
| D. | 若α∩β=b,a?α,则a与β一定相交. |
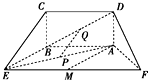 如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.
如图所示的五面体中,四边形ABCD是矩形,AD⊥平面ABEF,AB∥EF,且AD=1,AB=$\frac{1}{2}$EF=2$\sqrt{2}$,AF=BE=2,点P、Q、M分别为AE、BD、EF的中点.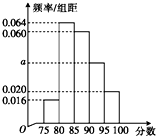 某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法抽取12人参加面试,则成绩在[90,100]内的学生应抽取的人数为6.
某高校在某年的自主招生考试成绩中随机抽取50名学生的笔试成绩,绘制成频率分布直方图如图所示,若要从成绩在[85,90),[90,95),[95,100]三组内的学生中,用分层抽样的方法抽取12人参加面试,则成绩在[90,100]内的学生应抽取的人数为6.