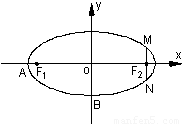
题目内容
已知椭圆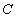 :
: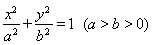 的左、右焦点分别为
的左、右焦点分别为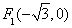 、
、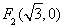 ,椭圆上的点
,椭圆上的点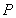 满足
满足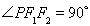 ,且△
,且△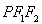 的面积为
的面积为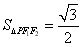 .
.
(Ⅰ)求椭圆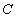 的方程;
的方程;
(Ⅱ)设椭圆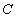 的左、右顶点分别为
的左、右顶点分别为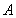 、
、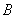 ,过点
,过点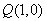 的动直线
的动直线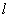 与椭圆
与椭圆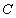 相交于
相交于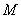 、
、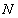 两点,直线
两点,直线 与直线
与直线 的交点为
的交点为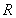 ,证明:点
,证明:点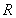 总在直线
总在直线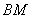 上.
上.
【答案】
(Ⅰ)椭圆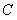 的方程为
的方程为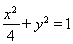 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)由焦点坐标知: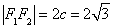 .又椭圆上的点
.又椭圆上的点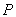 满足
满足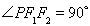 ,由
,由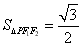 可求得
可求得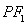 ,再由勾股定理可求得
,再由勾股定理可求得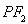 ,从而求得
,从而求得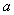 .再由
.再由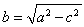 求得
求得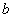 ,从而得椭圆的方程.(Ⅱ)首先考虑
,从而得椭圆的方程.(Ⅱ)首先考虑 与
与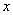 轴垂直的情况,此时可求出直线
轴垂直的情况,此时可求出直线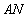 与直线
与直线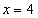 的交点为
的交点为 ,
,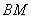 的方程是:
的方程是: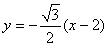 ,代入验证知点
,代入验证知点 在直线
在直线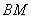 上.当直线
上.当直线 不与
不与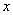 轴垂直时,设直线
轴垂直时,设直线 的方程为
的方程为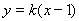 ,点
,点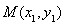 、
、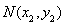 ,
,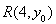 ,则
,则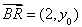 ,
,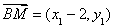 ,要证明
,要证明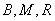 共线,只需证明
共线,只需证明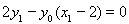 ,即证明
,即证明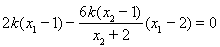 .
.
若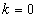 ,显然成立;若
,显然成立;若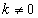 , 即证明
, 即证明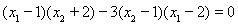
而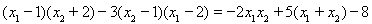 ,这显然用韦达定理.
,这显然用韦达定理.
试题解析:(Ⅰ)由题意知: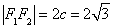 , 1分
, 1分
 椭圆上的点
椭圆上的点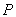 满足
满足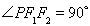 ,且
,且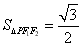 ,
,
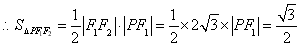 .
.
 ,
,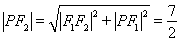 .
.
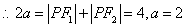 2分
2分
又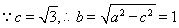 3分
3分
 椭圆
椭圆 的方程为
的方程为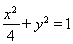 . 4分
. 4分
(Ⅱ)由题意知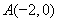 、
、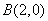 ,
,
(1)当直线 与
与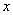 轴垂直时,
轴垂直时,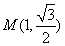 、
、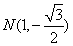 ,则
,则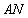 的方程是:
的方程是: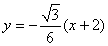 ,
,
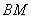 的方程是:
的方程是: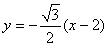 ,直线
,直线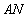 与直线
与直线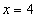 的交点为
的交点为 ,
,
∴点 在直线
在直线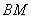 上. 6分
上. 6分
(2)当直线 不与
不与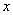 轴垂直时,设直线
轴垂直时,设直线 的方程为
的方程为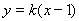 ,
,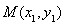 、
、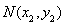 ,
,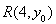
由 得
得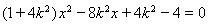
∴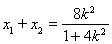 ,
,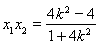 7分
7分
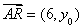 ,
,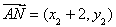 ,
, 共线,∴
共线,∴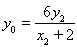 8分
8分
又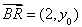 ,
,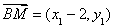 ,需证明
,需证明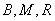 共线,
共线,
需证明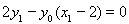 ,只需证明
,只需证明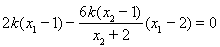
若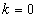 ,显然成立,若
,显然成立,若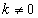 , 即证明
, 即证明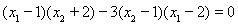
∵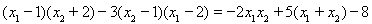
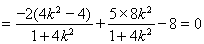 成立, 11分
成立, 11分
∴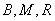 共线,即点
共线,即点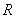 总在直线
总在直线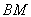 上. 12分
上. 12分
考点:1、椭圆的标准方程;2、直线与圆锥曲线.

练习册系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:

 的方程为
的方程为  ,双曲线
,双曲线 的左、右焦
的左、右焦 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的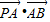 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.