[题目]已知双曲线C: 的左.右焦点分别为F1 . F2 . 点M与双曲线C的焦点不重合.点M关于F1 . F2的对称点分别为A.B.线段MN的中点在双曲线的右支上.若|AN|﹣|BN|=12.则a=( )A.3B.4C.5D.6 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知双曲线C：（a＞0，b＞0）的左、右焦点分别为F1 ， F2 ，点M与双曲线C的焦点不重合，点M关于F1 ， F2的对称点分别为A，B，线段MN的中点在双曲线的右支上，若|AN|﹣|BN|=12，则a=（）
A.3
B.4
C.5
D.6

【答案】A
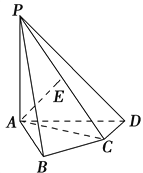
【解析】解：设双曲线C的左右焦点分别为F1 ， F2 ，如图，连接PF1 ， PF2 ，
∵F1是MA的中点，P是MN的中点，
∴F1P是△MAN的中位线，
∴|PF1|= |AN|，
同理|PF2|= |BN|，
∴||AN|﹣|BN||=2||PF1|﹣|PF2||，
∵P在双曲线上，
根据双曲线的定义知：||PF1|﹣|PF2||=2a，
∴||AN|﹣|BN||=4a=12，∴a=3．
故选A．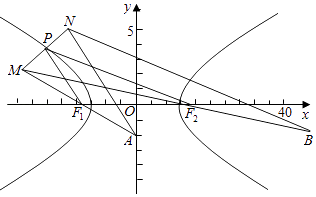

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

【题目】在心理学研究中，常采用对比试验的方法评价不同心理暗示对人的影响，具体方法如下：将参加试验的志愿者随机分成两组，一组接受甲种心理暗示，另一组接受乙种心理暗示，通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用，现有6名男志愿者A1 ， A2 ， A3 ， A4 ， A5 ， A6和4名女志愿者B1 ， B2 ， B3 ， B4 ，从中随机抽取5人接受甲种心理暗示，另5人接受乙种心理暗示．（12分）
（Ⅰ）求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率．
（Ⅱ）用X表示接受乙种心理暗示的女志愿者人数，求X的分布列与数学期望EX．

【题目】下列说法正确的是（）

A. 某厂一批产品的次品率为，则任意抽取其中10件产品一定会发现一件次品

B. 掷一枚硬币，连续出现5次正面向上，第六次出现反面向上的概率与正面向上的概率仍然都为0.5

C. 某医院治疗一种疾病的治愈率为10%，那么前9个病人都没有治愈，第10个人就一定能治愈

D. 气象部门预报明天下雨的概率是90%，说明明天该地区90%的地方要下雨，其余10%的地方不会下雨

【题目】如图，将边长为6的等边三角形各切去一个全等的四边形，再沿虚线折起，做成一个无盖的正三棱柱形的容器．

（1）若这个容器的底面边长为，容积为，写出关于的函数关系式并注明定义域；

（2）求这个容器容积的最大值．

【题目】如图，在四棱锥PABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．

(1)证明：AE⊥平面PCD；

(2)求二面角A－PD－C的正弦值．

【题目】某小区内有一块以为圆心半径为20米的圆形区域.广场，为丰富市民的业余文化生活，现提出如下设计方案：如图，在圆形区域内搭建露天舞台，舞台为扇形区域，其中两个端点，分别在圆周上；观众席为梯形内且在圆外的区域，其中，，且，在点的同侧.为保证视听效果，要求观众席内每一个观众到舞台处的距离都不超过60米.设.