题目内容
某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:


 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.

问:(1)求这40辆小型车辆车速的众数和中位数的估计值.(2)若从车速在 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).



 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.
问:(1)求这40辆小型车辆车速的众数和中位数的估计值.(2)若从车速在
 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).(1)众数的估计值等于 .中位数的估计值为:
.中位数的估计值为: ;
;
(2) 的分布列为:
的分布列为:
均值 .
.
 .中位数的估计值为:
.中位数的估计值为: ;
;(2)
 的分布列为:
的分布列为: | 0 | 1 | 2 |
 |  |  |  |
 .
. 试题分析:(1)众数的估计值为最高的矩形的中点;如下图,

设图中虚线所对应的车速为
 ,若
,若 两侧的矩形的面积相等,则这个
两侧的矩形的面积相等,则这个 就是中位数的估计值;
就是中位数的估计值;(2)首先看随机变量可以取哪些值?从图中可知,这40辆车中,车速在
 的车辆数为:
的车辆数为: 辆,车速在
辆,车速在 的车辆数为:
的车辆数为: 辆.所以
辆.所以 .显然这是一个超几何分布,由此可得其分布列及期望.
.显然这是一个超几何分布,由此可得其分布列及期望. 试题解析:(1)众数的估计值为最高的矩形的中点,即众数的估计值等于
 (2分)
(2分)
设图中虚线所对应的车速为
 ,则中位数的估计值为:
,则中位数的估计值为: ,解得
,解得
即中位数的估计值为
 (5分)
(5分)(2)从图中可知,车速在
 的车辆数为:
的车辆数为: (辆),
(辆),车速在
 的车辆数为:
的车辆数为: (辆) (7分)
(辆) (7分)∴
 ,
,  ,
, ,
, ,
, 的分布列为:
的分布列为: | 0 | 1 | 2 |
 |  |  |  |
均值
 . (12分
. (12分
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目

 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图: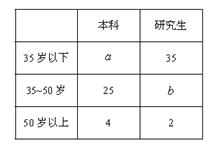
 ,求
,求 的值;
的值; 表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
表示编号为n(n=1,2,3, 、6)的同学所得成绩,且前5位同学的成绩如下:
 及这6位同学成绩的标准差s;
及这6位同学成绩的标准差s;


 ,
, ,
, ,
, ,
,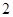 的方差为 .
的方差为 .