题目内容
某校有教职工 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
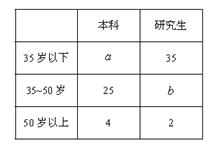
(Ⅰ)随机抽取一人,是35岁以下的概率为 ,求
,求 的值;
的值;
(Ⅱ)从50岁以上的6人中随机抽取两人,求恰好只有一位是研究生的概率.
 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
(Ⅰ)随机抽取一人,是35岁以下的概率为
 ,求
,求 的值;
的值;(Ⅱ)从50岁以上的6人中随机抽取两人,求恰好只有一位是研究生的概率.
(Ⅰ)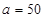 ,
,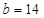 ;(Ⅱ)
;(Ⅱ)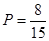 .
.
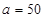 ,
,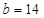 ;(Ⅱ)
;(Ⅱ)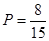 .
.试题分析:(Ⅰ)先根据已知条件“随机抽取一人,是35岁以下的概率为
 ”,得到
”,得到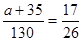 ,解出
,解出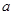 的值,再由总人数减去已知的所有的人数即是未知的
的值,再由总人数减去已知的所有的人数即是未知的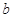 的值;(Ⅱ)将
的值;(Ⅱ)将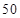 岁以上的
岁以上的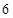 人进行编号,列举出所有满足“从这
人进行编号,列举出所有满足“从这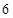 人中任取
人中任取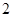 人”和“其中恰好有一位研究生”的基本事件的个数,然后求出“从50岁以上的6人中随机抽取两人,恰好只有一位是研究生”的概率.
人”和“其中恰好有一位研究生”的基本事件的个数,然后求出“从50岁以上的6人中随机抽取两人,恰好只有一位是研究生”的概率.试题解析:(Ⅰ)由已知得:
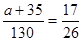 ,解得
,解得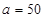 ,
,故
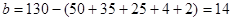 ,即
,即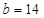 .
.(Ⅱ)将
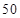 岁以上的
岁以上的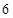 人进行编号:四位本科生为:
人进行编号:四位本科生为: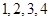 ,两位研究生为
,两位研究生为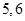 .
.从这
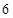 人中任取
人中任取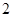 人共有
人共有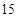 种等可能发生的基本事件,分别为:
种等可能发生的基本事件,分别为: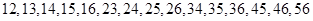 ,
,其中恰好有一位研究生的有
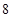 种,分别为:
种,分别为: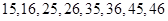 ,
,故所求的概率为:
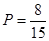 .
.
练习册系列答案
相关题目
 名同学,现测得排球队
名同学,现测得排球队 )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、



 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.
 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
 、
、 、
、 、
、 六段后得到如下频率分布表:
六段后得到如下频率分布表:






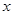







 的市民中抽取容量为
的市民中抽取容量为 人在分数段
人在分数段 ,
, ,
, ,
, ,
, 。
。
 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数
 之外的人数。
之外的人数。 :y
:y ,
, ,中位数分别为
,中位数分别为 ,
, ,则( )
,则( )
 ,
,

 ,
,
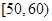 ,
, ,
, ,
, ,
, ,则这100名学生数学成绩在
,则这100名学生数学成绩在 分数段内的人数为( )
分数段内的人数为( )