Question

7．定义域为R的偶函数f（x）满足对?x∈R，有f（x+2）=f（x）-f（1），且当x∈[2，3]时，f（x）=-2x²+12x-18．若函数y=f（x）-log_a（|x|+1）在R上至少有四个零点，则a的取值范围是0＜a≤$\frac{\sqrt{3}}{3}$．

Answer 1

分析 可证偶函数f（x）的周期为2，可作出函数的图象，数形结合可得．

解答 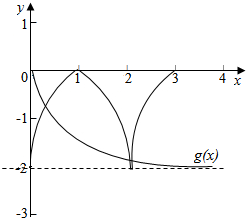解：∵f（x+2）=f（x）-f（1），且f（x）是定义域为R的偶函数，
令x=-1可得f（-1+2）=f（-1）-f（1），
由f（-1）=f（1）可得f（1）=0，
∴f（x+2）=f（x），∴f（x）是周期为2的偶函数，
当x∈[2，3]时，f（x）=-2x²+12x-18=-2（x-3）²，
图象为开口向下，顶点为（3，0）的抛物线，
∵函数y=f（x）-log_a（|x|+1）在R上至少有四个零点，
∵f（x）≤0，∴g（x）≤0，可得a＜1，
要使函数y=f（x）-log_a（|x|+1）在R上至少有四个零点，
令g（x）=log_a（|x|+1），则需g（2）≥f（2），
代值可得log_a（2+1）≥f（2）=-2，
∴可得log_a3≥-2，∴3≤$\frac{1}{{a}^{2}}$，解得-$\frac{\sqrt{3}}{3}$≤a≤$\frac{\sqrt{3}}{3}$，
又∵a＞0，∴0＜a≤$\frac{\sqrt{3}}{3}$，
故答案为：0＜a≤$\frac{\sqrt{3}}{3}$．

点评 本题考查函数的零点和周期性，涉及数形结合的方法，属中档题．