题目内容
【题目】过抛物线y2=2px(p>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线l作垂线,垂足分别为M1、N1.
(1)求![]() ;
;
(2)记△FMM1、△FM1N1、△FNN1的面积分别为![]() 、
、![]() 、
、![]() ,求
,求![]()
【答案】(1)0;(2)4
【解析】
(1)先表示出F,![]() 的坐标,再向量坐标化,表示出
的坐标,再向量坐标化,表示出![]() 的坐标,联立直线MN的方程和抛物线方程,根据韦达定理得到结果;(2)分别表示出面积表达式,S
的坐标,联立直线MN的方程和抛物线方程,根据韦达定理得到结果;(2)分别表示出面积表达式,S![]() =4
=4![]()
![]() (
(![]() p|
p|![]() -
-![]() |)
|)![]() =4×
=4×![]() (
(![]() +
+![]() )|
)|![]() |·
|·![]() (
(![]() +
+![]() )·|
)·|![]() |
|![]()
![]() [(
[(![]() +
+![]() )2-4
)2-4![]() ]=[
]=[![]() +
+![]() (
(![]() +
+![]() )+
)+ ![]() ]·|
]·|![]() |,联立直线和抛物线根据韦达定理得证即可.
|,联立直线和抛物线根据韦达定理得证即可.
.
(1)依题意,焦点为F(![]() ,0),准线l的方程为x=-
,0),准线l的方程为x=-![]() .
.
设点M,N的坐标分别为M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),直线MN的方程为x=my+
),直线MN的方程为x=my+![]() ,则有M1(-
,则有M1(-![]() ,
,![]() ),N1(-
),N1(-![]() ,
,![]() ),
),![]() =(-p,
=(-p,![]() ),
), ![]() =(-p,
=(-p,![]() ).
).
由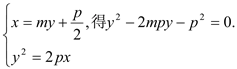
于是,![]() +
+![]() =2mp,
=2mp,![]() =-
=-![]() .
.
∴![]() ·
·![]() =
=![]() +
+![]() =
=![]() -
-![]() =0
=0
(2)S![]() =4
=4![]() 成立,证明如下:
成立,证明如下:
设M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
直线l与x轴的交点为![]() ,则由抛物线的定义得
,则由抛物线的定义得
|M M1|=|MF|=![]() +
+![]() , |N N1|=|NF|=
, |N N1|=|NF|=![]() +
+![]() . 于是
. 于是
![]() =
=![]() ·|M M1|·| F1 M1|=
·|M M1|·| F1 M1|=![]() (
(![]() +
+![]() )|
)|![]() |,
|,
![]() =
=![]() ·| M1 N1|·|F F1|=
·| M1 N1|·|F F1|=![]() p|
p|![]() -
-![]() |,
|,
![]() =
=![]() ·|N N1|·| F1 N1|=
·|N N1|·| F1 N1|=![]() (
(![]() +
+![]() )|
)|![]() |,
|,
∵S![]() =4
=4![]()
![]() (
(![]() p|
p|![]() -
-![]() |)
|)![]() =4×
=4×![]() (
(![]() +
+![]() )|
)|![]() |·
|·![]() (
(![]() +
+![]() )·|
)·|![]() |
|![]()
![]()
![]() [(
[(![]() +
+![]() )
)![]() -4
-4![]() ]=[
]=[![]() +
+![]() (
(![]() +
+![]() )+
)+![]() ]·|
]·|![]() |.
|.
将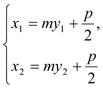 与
与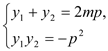 代入上式化简可得
代入上式化简可得![]() 此式恒成立. 故
此式恒成立. 故![]() =4.
=4.

【题目】自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元. 
(Ⅰ)求该企业2016年一年生产一件产品的利润的分布列和期望;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.


