题目内容
(本小题满分13分)已知椭圆的中心在原点,焦点在y轴上,离心率为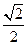 ,且
,且
椭圆经过圆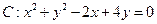 的圆心C。
的圆心C。
(I)求椭圆的标准方程;
(II)设直线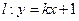 与椭圆交于A、B两点,点
与椭圆交于A、B两点,点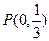 且|PA|=|PB|,求直线
且|PA|=|PB|,求直线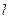 的方程。
的方程。
(1)由圆C的方程可知:圆心C(1,-2) ————2分
设椭圆的方程为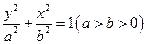
椭圆过圆心C,可得: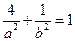
另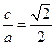 ,且
,且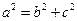 。
。
解得: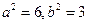
即椭圆的方程为: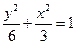 ————6分
————6分
(2)将直线方程与椭圆方程联立方程组消元可得: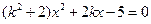
设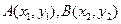
法一:设AB中点M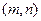
其中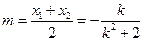 ,
, ————8分
————8分
若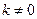 ,则有:
,则有: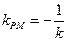 ,解得:
,解得: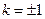 ————10分
————10分
若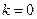 ,显然满足题意。
,显然满足题意。
故直线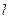 的方程为:
的方程为: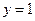 或
或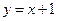 或
或 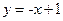 ————13分
————13分
法二:由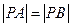 ,代入可得方程:可解出
,代入可得方程:可解出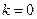 或
或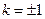
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知椭圆 、抛物线
、抛物线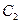 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和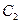 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 | 3 |  2 2 | 4 |  |
 |  | 0 |  4 4 |  |
 的标准方程;
的标准方程;(Ⅱ)请问是否存在直线
 满足条件:①过
满足条件:①过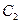 的焦点
的焦点 ;②与
;②与 交不同两点
交不同两点 且满足
且满足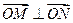 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. 在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( )
A.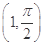 | B.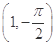 | C.(1,0) | D.(1,π) |
在极坐标系中,圆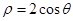 的垂直于极轴的两条切线方程分别为( )
的垂直于极轴的两条切线方程分别为( )
A.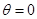 ( (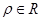 )和 )和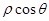 =2 =2 |
B.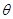 = =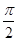 ( (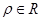 )和 )和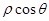 =2 =2 |
C.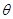 = =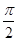 ( (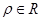 )和 )和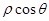 =1 =1 |
D.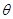 =0( =0(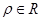 )和 )和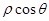 =1 =1 |
在极坐标系中,点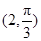 和圆
和圆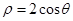 的圆心的距离为( )
的圆心的距离为( )
A.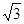 | B. 2 | C.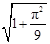 | D.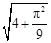 |
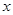 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).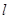 与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线
与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线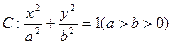 过点P
过点P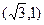 ,且离心率为
,且离心率为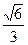 ,F为椭圆的右焦点,
,F为椭圆的右焦点,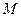 、
、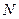 两点在椭圆
两点在椭圆 上,且
上,且 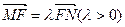 ,定点
,定点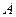 (-4,0).
(-4,0).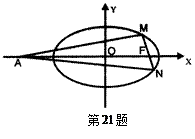
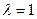 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论.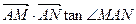 =6
=6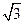 时
时 , 求直线MN的方程.
, 求直线MN的方程. 2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则
2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则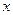 轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐
轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐 ,过点
,过点 ,过点
,过点 ,交线段
,交线段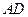 于点
于点 ,连接
,连接 ,使
,使 ~
~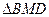 ,若存在,求出点
,若存在,求出点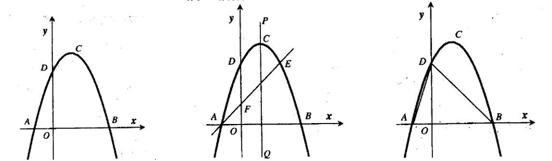 图1 图2
图1 图2  图3
图3 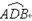 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.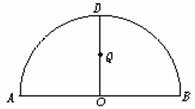
 l与曲线C相交于不同的两点M、N,且M在D、N之间,设
l与曲线C相交于不同的两点M、N,且M在D、N之间,设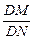 =λ,求λ的取值范围.
=λ,求λ的取值范围.