题目内容
在极坐标系中,圆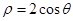 的垂直于极轴的两条切线方程分别为( )
的垂直于极轴的两条切线方程分别为( )
A.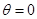 ( (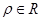 )和 )和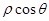 =2 =2 |
B.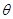 = =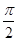 ( (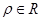 )和 )和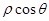 =2 =2 |
C.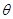 = =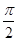 ( (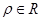 )和 )和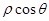 =1 =1 |
D.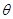 =0( =0(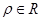 )和 )和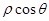 =1 =1 |
B
解析试题分析:将圆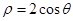 的方程互为直角坐标方程为
的方程互为直角坐标方程为 ,圆心为(1,0)半径为1,故垂直于极轴的两条切线方程分别为
,圆心为(1,0)半径为1,故垂直于极轴的两条切线方程分别为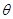 =
=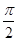 (
(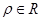 )和
)和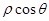 =2,故选B.
=2,故选B.
考点:直角坐标方程与极坐标方程互化;圆的切线方程

练习册系列答案
相关题目
若曲线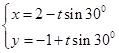 (
( 为参数) 与曲线
为参数) 与曲线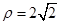 相交于
相交于 ,
, 两点,则
两点,则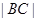 的值为( ).
的值为( ).
A.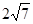 | B.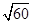 | C.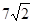 | D.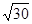 |
已知曲线M与曲线N:ρ=5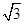 cosθ-5sinθ关于极轴对称,则曲线M的方程为( )
cosθ-5sinθ关于极轴对称,则曲线M的方程为( )
A.ρ=-10cos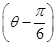 | B.ρ=10cos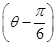 |
C.ρ=-10cos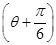 | D.ρ=10cos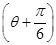 |
设r>0,那么直线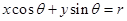 (
(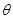 是常数)与圆
是常数)与圆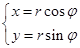 (
(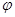 是参数)的位置关系是
是参数)的位置关系是
| A.相交 | B.相切 | C.相离 | D.视r的大小而定 |
设点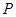 对应的复数为
对应的复数为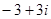 ,以原点为极点,实轴正半轴为极轴建立极坐标系,则点
,以原点为极点,实轴正半轴为极轴建立极坐标系,则点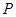 的极坐标可能为( )
的极坐标可能为( )
A.(3,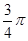 ) ) | B.(3,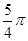 ) ) | C.( , ,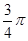 ) ) | D.( , ,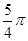 ) ) |
在平面直角坐标系中,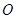 为原点,
为原点,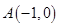 ,
,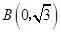 ,
,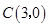 ,动点
,动点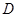 满足
满足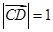 ,
,
则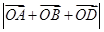 的取值范围是( )
的取值范围是( )
A.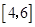 | B.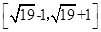 |
C.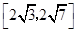 | D.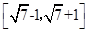 |
在极坐标系中,直线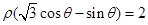 与圆
与圆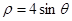 的交点的极坐标为( )
的交点的极坐标为( )
A.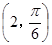 | B.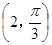 | C.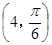 | D.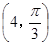 |
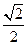 ,且
,且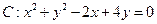 的圆心C。
的圆心C。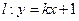 与椭圆交于A、B两点,点
与椭圆交于A、B两点,点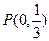 且|PA|=|PB|,求直线
且|PA|=|PB|,求直线 的方程。
的方程。 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有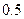 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽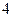 米,车高
米,车高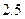 米.
米. 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行?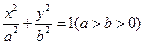 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?