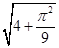题目内容
(12分) 如图, 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.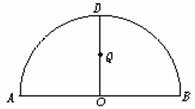
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线 l与曲线C相交于不同的两点M、N,且M在D、N之间,设
l与曲线C相交于不同的两点M、N,且M在D、N之间,设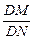 =λ,求λ的取值范围.
=λ,求λ的取值范围.
.解:(1)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,?∵|PA|+|PB|=|QA|+|QB| =2
=2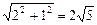 >|AB|=4.
>|AB|=4.
∴曲线C为以原点为中心,A、B为焦点的椭圆. ……2分
设其长半轴为a,短半轴为b,半焦距为c,则2a=2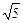 ,∴a=
,∴a=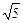 ,c=2,b=1.
,c=2,b=1.
∴曲线C的方程为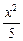 +y2="1. "
+y2="1. "  ……4分
……4分
(2)设直线l的方程为y=kx+2,
代入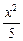 +y2=1,得(1+5k2)x2+20kx+15=0.
+y2=1,得(1+5k2)x2+20kx+15=0.
Δ=(20k)2-4×15(1+5k2)>0,得k2>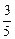 .由图可知
.由图可知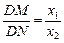 =λ
=λ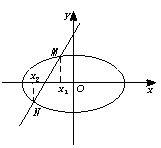
由韦达定理得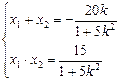 ……6分
……6分
将x1=λx2代入得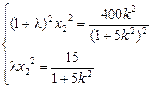
两式相除 得
得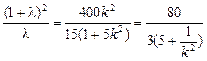 ……8分
……8分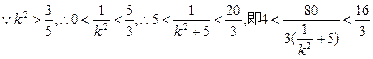
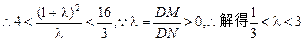 ①
①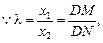 M在D、N中间,∴λ<1
M在D、N中间,∴λ<1  ②又∵当k不存在时,显然λ=
②又∵当k不存在时,显然λ=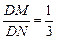 (此时直线l与y轴重合).
(此时直线l与y轴重合).
所以,所求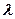 的取值范围是
的取值范围是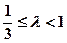 . ……12分
. ……12分
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案已知曲线M与曲线N:ρ=5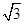 cosθ-5sinθ关于极轴对称,则曲线M的方程为( )
cosθ-5sinθ关于极轴对称,则曲线M的方程为( )
A.ρ=-10cos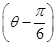 | B.ρ=10cos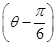 |
C.ρ=-10cos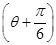 | D.ρ=10cos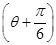 |
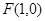 ,直线
,直线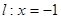 ,
,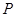 为平面上的动点,过
为平面上的动点,过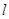 的垂线,垂足为点
的垂线,垂足为点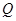 ,且
,且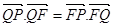 .
.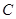 的方程;
的方程;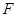 的直线交轨迹
的直线交轨迹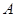 ,
,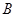 两点,交直线
两点,交直线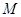 ,已知
,已知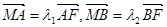 ,求
,求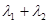 的值.
的值.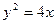 ,过点
,过点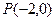 的直线AB交抛物线于点
的直线AB交抛物线于点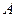 、
、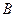 ,若线段
,若线段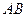 的垂直平分线交
的垂直平分线交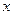 轴于点
轴于点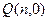 ,求
,求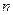 的取值范围.
的取值范围.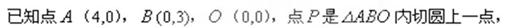
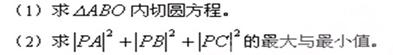
 的准线为
的准线为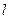 ,焦点为
,焦点为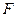 ,圆
,圆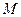 的圆心在
的圆心在 轴的正半轴上,且与
轴的正半轴上,且与 轴相切,过原点
轴相切,过原点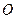 作倾斜角为
作倾斜角为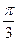 的直线
的直线 ,交
,交 于点
于点 ,交圆
,交圆 ,且
,且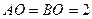
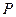 为抛物线C上的动点,求
为抛物线C上的动点,求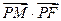 的最小值;
的最小值; 恒过一个定点,并求该定点的坐标.
恒过一个定点,并求该定点的坐标.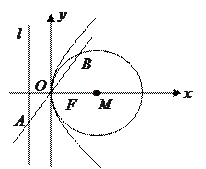
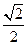 ,且
,且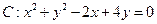 的圆心C。
的圆心C。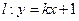 与椭圆交于A、B两点,点
与椭圆交于A、B两点,点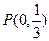 且|PA|=|PB|,求直线
且|PA|=|PB|,求直线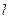 的方程。
的方程。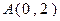 ,右焦点
,右焦点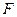 与点
与点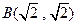 的距离为
的距离为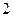 .
.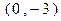 的直线
的直线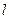 ,使直线
,使直线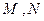 满足
满足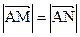 ?若存在,求出直线
?若存在,求出直线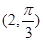 到圆
到圆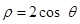 的圆心的距离为( ).
的圆心的距离为( ).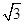 C.
C. 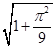 D
D