题目内容
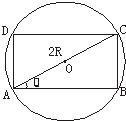
求半径为R的圆的内接矩形周长的最大值．
【答案】分析：设∠BAC=θ，周长为P，则可用θ的三角函数表示出AB和BC，进而整理后根据正弦函数的性质求的周长的最大值．
解答：解：设∠BAC=θ，周长为P，
则P=2AB+2BC=2（2Rcosθ+2Rsinθ）=4
Rsin（θ+
）≤4
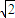R，
当且仅当θ=
时，取等号．
∴周长的最大值为4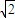
R．
点评：本题主要考查了基本不等式在最值问题中的应用．本题利用了三角函数的性质来求最值．
解答：解：设∠BAC=θ，周长为P，
则P=2AB+2BC=2（2Rcosθ+2Rsinθ）=4
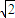Rsin（θ+）≤4R，当且仅当θ=
时，取等号．∴周长的最大值为4
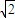R．点评：本题主要考查了基本不等式在最值问题中的应用．本题利用了三角函数的性质来求最值．
练习册系列答案
相关题目
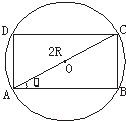求半径为R的圆的内接矩形周长的最大值．
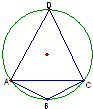在半径为R的圆的内接四边形ABCD中，AB=
