题目内容
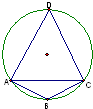 在半径为R的圆的内接四边形ABCD中,AB=
在半径为R的圆的内接四边形ABCD中,AB=| 3 |
| 3 |
| 1 |
| 4 |
(1)圆的半径R;
(2)
| DA |
| DC |
(3)四边形ABCD的周长.
分析:(1)求半径有如下方法:构造含半径R的三角形,解三角形求出半径R值;或是根据正弦定理,
=
=
=2R,根据本题的已知条件,可知用正弦定理相对可行,故可由余弦定理求出AC,再由正弦定理求R.
(2)要求
•
,根据向量数量积的计算公式,我们要求出两个向量模的积及夹角的余弦值,由∠B与∠D互补,夹角的余弦值易得,然后根据△ACD的面积等于△ABC面积的3倍,也可以得到两个向量模的积,代入可得答案.
(3)由AB=
-1,BC=
+1,我们要求四边形的周长,关键是要求出AD、CD边的长,结合(2)结论和余弦定理,易得答案.
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
(2)要求
| DA |
| DC |
(3)由AB=
| 3 |
| 3 |
解答:解:(1)在三角形ABC中,
有余弦定理:AC2=AB2+BC2-2AB•BCcos∠ABC,
∵AB=
-1,BC=
+1,cos∠ABC=-
,
所以AC=3,
由正弦定理可知:
=2R=
,
∴R=
;
(2)
•
=|DA|•|DC|cos∠ADC=
|DA|•|DC|,
因为△ACD的面积等于△ABC面积的3倍,
即
•DA•DC•sin∠ADC=3•
•BA•BC•sin∠ABC
∴DA•DC=3BA•BC,
∵BA•BC=2,
∴
•
=
;
(3)三角形ADC中,有AC2=AD2+CD2-2AD•CDcos∠DAC,
又∵DA•DC=6,所以有AD2+AC2=12,
从而有DA+DC=2
,
所以四边形ABCD的周长为2
+2
.
有余弦定理:AC2=AB2+BC2-2AB•BCcos∠ABC,
∵AB=
| 3 |
| 3 |
| 1 |
| 4 |
所以AC=3,
由正弦定理可知:
| AC |
| sin∠ABC |
| 3 | ||||
|
∴R=
2
| ||
| 5 |
(2)
| DA |
| DC |
| 1 |
| 4 |
因为△ACD的面积等于△ABC面积的3倍,
即
| 1 |
| 2 |
| 1 |
| 2 |
∴DA•DC=3BA•BC,
∵BA•BC=2,
∴
| DA |
| DC |
| 3 |
| 2 |
(3)三角形ADC中,有AC2=AD2+CD2-2AD•CDcos∠DAC,
又∵DA•DC=6,所以有AD2+AC2=12,
从而有DA+DC=2
| 6 |
所以四边形ABCD的周长为2
| 6 |
| 3 |
点评:此题考查了正弦定理,余弦定理,三角形的面积公式以及平面向量的数量积运算,求圆的半径有如下方法:①构造含半径R的三角形,解三角形求出半径R值;②如果圆为△ABC的外接圆,则根据正弦定理,
=
=
=2R;③如果圆为△ABC的内切圆,则根据面积公式S=
•l•r(其中l表示三角形的周长).熟练掌握定理及公式是解本题的关键.
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
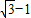 ,BC=
,BC=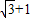 ,
,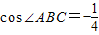 ,且△ACD的面积等于△ABC面积的3倍,求:
,且△ACD的面积等于△ABC面积的3倍,求: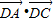 的值;
的值;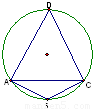
 .通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .
.通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .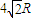 .通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .
.通过类比,我们可得结论:在空间,半径为R的球的内接长方体中,以 的表面积为最大,最大值为 .