题目内容
16.定义在R上的函数f(x)满足:f(x)+f′(x)>1,f(0)=5,则不等式exf(x)>4+ex的解集为( )| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (-∞,0)∪(3,+∞) | D. | (-∞,0) |
分析 构造函数g(x)=exf(x)-ex,(x∈R),研究g(x)的单调性,结合原函数的性质和函数值,解出即可.
解答 解:设g(x)=exf(x)-ex,(x∈R),
则g′(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1],
∵f′(x)+f(x>1,
∴f(x)+f′(x)-1>0,
∴g′(x)>0,
∴y=g(x)在定义域上单调递增,
∵exf(x)>ex+4,∴g(x)>4,
又∵g(0)=e0f(0)-e0=5-1=4,
∴g(x)>g(0),
∴x>0,
∴不等式的解集为(0,+∞)
故选:B.
点评 本题考查函数单调性与奇偶性的结合,结合已知条件构造函数,然后用导数判断函数的单调性是解题的关键.

练习册系列答案
相关题目
7.已知数列{an}的通项公式an=$\frac{n+1}{n+2}$(n∈N+),设{an}的前n项积为sn,则使sn<$\frac{1}{32}$成立的自然数n( )
| A. | 有最大值62 | B. | 有最小值63 | C. | 有最大值62 | D. | 有最小值31 |
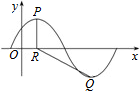 已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$
已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$ 已知函数$f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.