题目内容
已知椭圆![]() 的长轴长为4,且点
的长轴长为4,且点![]() 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)过椭圆右焦点的直线l交椭圆于A,B两点,若以AB为直径的圆过原点,求直线l方程.
答案:
解析:
解析:
|
解:(Ⅰ)由题意: 又点 (Ⅱ)由(Ⅰ)知 因为以 若直线 直线AB交椭圆于 若直线 由 由于直线 |

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
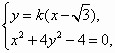 可得
可得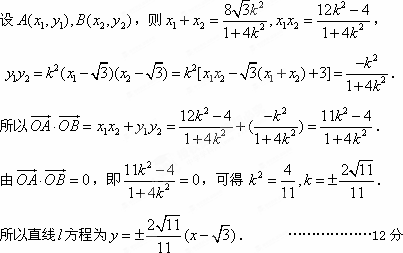

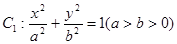 的长轴长为4,离心率为
的长轴长为4,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点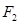 ,且与直线
,且与直线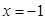 相切.
相切.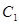 的方程;
(ⅱ)求动圆圆心
的方程;
(ⅱ)求动圆圆心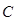 的轨迹方程;
的轨迹方程; ,椭圆
,椭圆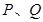 ,满足
,满足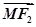 与
与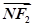 共线,
共线,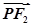 与
与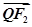 共线,且
共线,且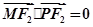 ,求四边形
,求四边形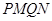 面积的最小值.
面积的最小值.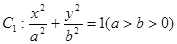 的长轴长为4,离心率为
的长轴长为4,离心率为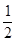 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点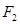 ,且与直线
,且与直线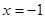 相切.
相切. 的方程; (ⅱ)求动圆圆心
的方程; (ⅱ)求动圆圆心 轨迹的方程;
轨迹的方程;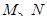 ,椭圆
,椭圆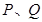 ,满足
,满足 与
与 共线,
共线,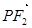 与
与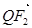 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值.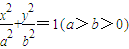 的长轴长为4,且点
的长轴长为4,且点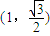 在该椭圆上.
在该椭圆上.