题目内容
已知椭圆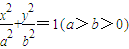 的长轴长为4,且点
的长轴长为4,且点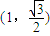 在该椭圆上.
在该椭圆上.(1)求椭圆的方程.
(2)过椭圆右焦点的直线l交椭圆于A、B两点,若∠AOB是直角,其中O是坐标原点,求直线l的方程.
【答案】分析:(1)由椭圆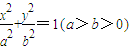 的长轴长为4,且点
的长轴长为4,且点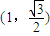 在该椭圆上,知
在该椭圆上,知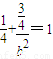 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.
(2)由直线l过椭圆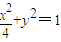 的右焦点F(
的右焦点F(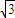 ,0),设l的方程为:y=k(x-
,0),设l的方程为:y=k(x-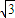 ),联立
),联立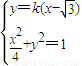 ,得(4k2+1)x2-8
,得(4k2+1)x2-8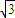 k2x+12k2-4=0,设A(x1,y1),B(x2,y2),由∠AOB是直角,利用韦达定理和x1x2+y1y2=0能求出直线l的方程.
k2x+12k2-4=0,设A(x1,y1),B(x2,y2),由∠AOB是直角,利用韦达定理和x1x2+y1y2=0能求出直线l的方程.
解答:解:(1)∵椭圆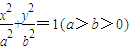 的长轴长为4,且点
的长轴长为4,且点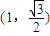 在该椭圆上,
在该椭圆上,
∴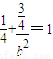 ,解得b2=1.
,解得b2=1.
∴椭圆的方程为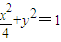 .
.
(2)∵直线l过椭圆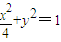 的右焦点F(
的右焦点F(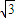 ,0),
,0),
∴设l的方程为:y=k(x-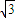 ),
),
联立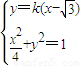 ,得(4k2+1)x2-8
,得(4k2+1)x2-8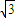 k2x+12k2-4=0,
k2x+12k2-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=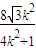 ,x1x2=
,x1x2=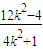 ,
,
y1y2=k(x1-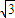 )•k(x2-
)•k(x2-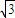 )=k2x1x2-
)=k2x1x2-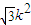 (x1+x2)+3k2,
(x1+x2)+3k2,
∵∠AOB是直角,
∴x1x2+y1y2=(k2+1)x1x2-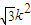 (x1+x2)+3k2
(x1+x2)+3k2
=(k2+1)•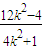 )-
)-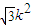 •
•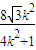 +3k2
+3k2
=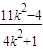 =0,
=0,
解得k=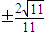 .
.
∴直线l的方程为y=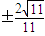 (x-
(x- ).
).
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意韦达定理、直线方程、椭圆性质、向量等知识点的合理运用.
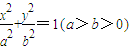 的长轴长为4,且点
的长轴长为4,且点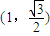 在该椭圆上,知
在该椭圆上,知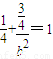 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.(2)由直线l过椭圆
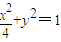 的右焦点F(
的右焦点F(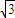 ,0),设l的方程为:y=k(x-
,0),设l的方程为:y=k(x-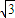 ),联立
),联立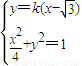 ,得(4k2+1)x2-8
,得(4k2+1)x2-8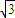 k2x+12k2-4=0,设A(x1,y1),B(x2,y2),由∠AOB是直角,利用韦达定理和x1x2+y1y2=0能求出直线l的方程.
k2x+12k2-4=0,设A(x1,y1),B(x2,y2),由∠AOB是直角,利用韦达定理和x1x2+y1y2=0能求出直线l的方程.解答:解:(1)∵椭圆
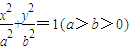 的长轴长为4,且点
的长轴长为4,且点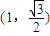 在该椭圆上,
在该椭圆上,∴
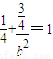 ,解得b2=1.
,解得b2=1.∴椭圆的方程为
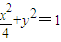 .
.(2)∵直线l过椭圆
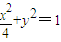 的右焦点F(
的右焦点F(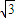 ,0),
,0),∴设l的方程为:y=k(x-
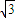 ),
),联立
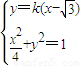 ,得(4k2+1)x2-8
,得(4k2+1)x2-8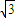 k2x+12k2-4=0,
k2x+12k2-4=0,设A(x1,y1),B(x2,y2),则x1+x2=
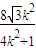 ,x1x2=
,x1x2=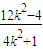 ,
,y1y2=k(x1-
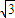 )•k(x2-
)•k(x2-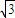 )=k2x1x2-
)=k2x1x2-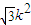 (x1+x2)+3k2,
(x1+x2)+3k2,∵∠AOB是直角,
∴x1x2+y1y2=(k2+1)x1x2-
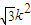 (x1+x2)+3k2
(x1+x2)+3k2=(k2+1)•
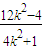 )-
)-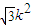 •
•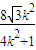 +3k2
+3k2=
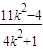 =0,
=0,解得k=
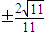 .
.∴直线l的方程为y=
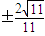 (x-
(x- ).
).点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意韦达定理、直线方程、椭圆性质、向量等知识点的合理运用.

练习册系列答案
相关题目

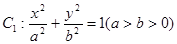 的长轴长为4,离心率为
的长轴长为4,离心率为 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点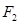 ,且与直线
,且与直线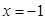 相切.
相切.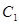 的方程;
(ⅱ)求动圆圆心
的方程;
(ⅱ)求动圆圆心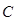 的轨迹方程;
的轨迹方程; ,椭圆
,椭圆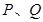 ,满足
,满足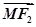 与
与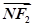 共线,
共线,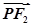 与
与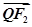 共线,且
共线,且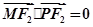 ,求四边形
,求四边形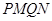 面积的最小值.
面积的最小值.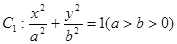 的长轴长为4,离心率为
的长轴长为4,离心率为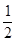 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点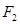 ,且与直线
,且与直线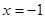 相切.
相切. 的方程; (ⅱ)求动圆圆心
的方程; (ⅱ)求动圆圆心 轨迹的方程;
轨迹的方程;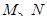 ,椭圆
,椭圆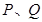 ,满足
,满足 与
与 共线,
共线,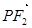 与
与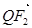 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值.