题目内容
(本小题满分12分)
已知椭圆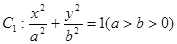 的长轴长为4,离心率为
的长轴长为4,离心率为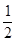 ,
, 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点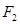 ,且与直线
,且与直线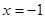 相切.
相切.
(Ⅰ)(ⅰ)求椭圆 的方程; (ⅱ)求动圆圆心
的方程; (ⅱ)求动圆圆心 轨迹的方程;
轨迹的方程;
(Ⅱ) 在曲线上 有两点
有两点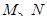 ,椭圆
,椭圆 上有两点
上有两点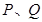 ,满足
,满足 与
与 共线,
共线,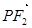 与
与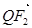 共线,且
共线,且 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
【答案】
解:(Ⅰ)(ⅰ)由已知可得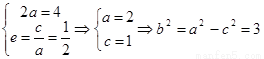 ,
,
则所求椭圆方程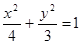 . ------------------------2分
. ------------------------2分
(ⅱ)由已知可得动圆圆心轨迹为抛物线,且抛物线 的焦点为(1,0),准线方程为
的焦点为(1,0),准线方程为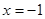 ,则动圆圆心轨迹方程为
,则动圆圆心轨迹方程为 . ----------------------------6分
. ----------------------------6分
(Ⅱ)当直线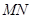 的斜率不存在时,
的斜率不存在时,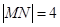 ,
,
此时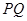 的长即为椭圆长轴长,
的长即为椭圆长轴长,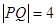 ,从而
,从而
设直线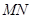 的斜率为
的斜率为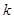 ,则
,则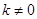 ,直线
,直线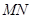 的方程为:
的方程为: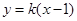
直线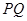 的方程为
的方程为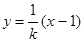 . 设
. 设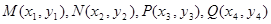
由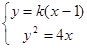 ,消去
,消去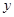 可得
可得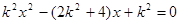
由抛物线定义可知:
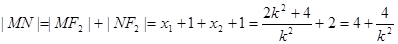 -------------------9分
-------------------9分
由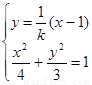 消去
消去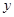 得
得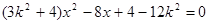 ,
,
从而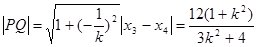
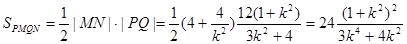
令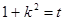 ,∵
,∵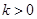 则
则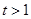 ,则
,则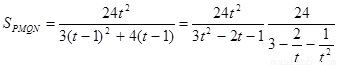
因为 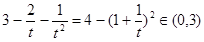 , 所以
, 所以
所以四边形PMQN面积的最小值为8 ------------------------------12分
【解析】略

练习册系列答案
相关题目