题目内容
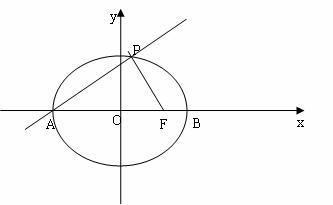
(13分)已知椭圆![]() 的长轴长为4,A,B,C是椭圆上的三点,点A是长轴的一个顶点,BC过椭圆的中心O,且
的长轴长为4,A,B,C是椭圆上的三点,点A是长轴的一个顶点,BC过椭圆的中心O,且![]() ,
,![]() ,如图.
,如图.
(Ⅰ)求椭圆的方程;
(Ⅱ)如果椭圆上的两点P,Q使![]() 的平分线垂直于OA,是否总存在实数
的平分线垂直于OA,是否总存在实数![]() ,使得
,使得![]() ?请说明理由.
?请说明理由.

解析:(Ⅰ)由题意知:![]() ,
,![]() ,
,
则椭圆方程为![]() …………………………………………………………………2分
…………………………………………………………………2分
由椭圆的对称性知:![]() ,
,
又![]()
![]() ,即
,即![]() 为等腰直角三角形,………………………4分
为等腰直角三角形,………………………4分
由![]() 得:
得:![]() ,代入椭圆方程得:
,代入椭圆方程得:![]() ,
,
即椭圆方程为![]() ;………………………………………………………………6分
;………………………………………………………………6分
(Ⅱ)假设总存在实数![]() ,使得
,使得![]() ,即
,即![]() ,……………………………7分
,……………………………7分
由![]() 得
得![]() ,则
,则![]() ,………………………………………8分
,………………………………………8分
若设CP:![]() ,则CQ:
,则CQ:![]() ,
,
由 ,………………9分
,………………9分
由![]() 得
得![]() 是方程
是方程![]() 的一个根,
的一个根,
由韦达定理得:![]() ,以
,以![]() 代k得
代k得![]() ,…10分
,…10分
故![]() ,故
,故![]() , ………………13分
, ………………13分

练习册系列答案
相关题目
 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为 ,若椭圆的焦点在
,若椭圆的焦点在 轴上,求椭圆的方程.
轴上,求椭圆的方程. 的中心在原点
的中心在原点 ,焦点
,焦点 ,
,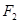 在
在 轴上,经过点
轴上,经过点 ,
, ,且抛物线
,且抛物线
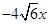 的焦点为
的焦点为 的直线
的直线 与椭圆
与椭圆 ,
, 两点,当以
两点,当以 为直径的圆
为直径的圆 与
与 轴相切时,求直线
轴相切时,求直线 的右焦点为
的右焦点为 ,
, 为椭圆的上顶点,
为椭圆的上顶点,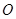 为坐标原点,且△
为坐标原点,且△ 是等腰直角三角形.
是等腰直角三角形.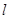 交椭圆于
交椭圆于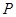 ,
, 两点,
且使点
两点,
且使点 为△
为△ 的垂心(垂心:三角形三边高线的交点)?若存在,求出直线
的垂心(垂心:三角形三边高线的交点)?若存在,求出直线 的离心率为
的离心率为 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线 相切,
相切,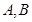 分别是椭圆的左右两个顶点,
分别是椭圆的左右两个顶点,  为椭圆
为椭圆 上的动点.
上的动点.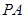 与
与 的斜率分别为
的斜率分别为 ,证明:
,证明: 为定值;
为定值;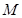 为过
为过 轴的直线上的点,若
轴的直线上的点,若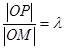 ,求点
,求点