题目内容
4．
已知函数y=f（x）的定义域为R，f（x）的导函数f′（x）的图象如图所示，则下列结论一定成立的是（ ）| A． | 函数f（x）在x=4处取得极值 | B． | f（1）＞f（2） | ||
| C． | 函数f（x）的最小值为0 | D． | f（2）-f（1）＜f′（1） |
分析 根据导函数的图象可知f（x）在R上为增函数，所以无最值、无极值，并且x=4是f（x）图象的拐点，所以可以了解函数f（x）图象的变化趋势，以及图象的大致形状，从而可判断f（x）在x=1处切线的斜率大于点（1，f（1）），和点（2，f（2））两点连线的斜率，从而判断出D是正确的．
解答 解：在x=4两边的导数都大于0，所以f（x）在x=4处取不到极值；
∴A错误；
根据导函数的图象知f′（x）≥0；
∴f（x）在R上单调递增；
∴f（1）＜f（2），f（x）在R上无最值；
∴B，C错误；
根据导函数的图象知道f（x）是曲线，并且x=4是f（x）图象的拐点；
∴根据f（x）图象的变化趋势知：f（x）在x=1处的切线斜率大于两点（1，f（1）），（2，f（2））连线的斜率；
∴$\frac{f（2）-f（1）}{2-1}＜f′（1）$；
∴D正确；
故选：D．
点评 考查函数导数符号和函数单调性的关系，若一个函数在R上单调，则它无最值和极值，最值和极值的概念，拐点的定义，以及根据图象判断切线和割线的斜率的大小关系．
练习册系列答案
阅读快车系列答案
相关题目
12．已知抛物线$x=\frac{1}{2}{y^2}$上一点P的横坐标为1，则点P到该抛物线的焦点F的距离为（ ）
| A． | $\frac{9}{8}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | $\frac{5}{4}$ |
已知函数f（x）的导函数f′（x）的图象如图所示，那么函数f（x）的图象最有可能的是图中的（ ）
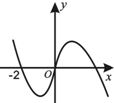
如图所示的是y=f′（x） 的图象，则下列判断正确的是（ ）