题目内容
若函数f（x）=|2x+a|的单调递增区间是[3，+∞），则a=________．
-6
分析：根据函数f（x）=|2x+a|关于直线
对称，单调递增区间是[3，+∞），可建立方程，即可求得a的值．
解答：∵函数f（x）=|2x+a|关于直线对称，单调递增区间是[3，+∞），
∴
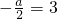
∴a=-6
故答案为：-6
点评：本题考查绝对值函数，考查函数的单调性，解题的关键是确定函数的对称轴，属于基础题．
分析：根据函数f（x）=|2x+a|关于直线
对称，单调递增区间是[3，+∞），可建立方程，即可求得a的值．解答：∵函数f（x）=|2x+a|关于直线
对称，单调递增区间是[3，+∞），∴
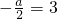
∴a=-6
故答案为：-6
点评：本题考查绝对值函数，考查函数的单调性，解题的关键是确定函数的对称轴，属于基础题．
练习册系列答案
相关题目
若函数f（x）=2-|x|-x2+a有两个不同的零点，则实数a的取值范围是（ ）
| A、[1，+∞） | B、（1，+∞） | C、[-1，+∞） | D、（-1，+∞） |