题目内容
【题目】已知函数![]() ,函数
,函数![]() 在点
在点![]() 处的切线斜率为0.
处的切线斜率为0.
(1)试用含有![]() 的式子表示
的式子表示![]() ,并讨论
,并讨论![]() 的单调性;
的单调性;
(2)对于函数![]() 图象上的不同两点
图象上的不同两点![]() ,
,![]() ,如果在函数
,如果在函数![]() 图象上存在点
图象上存在点![]() ,使得在点
,使得在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“跟随切线”.特别地,当
存在“跟随切线”.特别地,当![]() 时,又称
时,又称![]() 存在“中值跟随切线”.试问:函数
存在“中值跟随切线”.试问:函数![]() 上是否存在两点
上是否存在两点![]() 使得它存在“中值跟随切线”,若存在,求出
使得它存在“中值跟随切线”,若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(1)![]() ,单调性见解析;(2)不存在,理由见解析
,单调性见解析;(2)不存在,理由见解析
【解析】
(1)由题意得![]() ,即可得
,即可得![]() ;求出函数
;求出函数![]() 的导数
的导数![]() ,再根据
,再根据![]() 、
、![]() 、
、![]() 、
、![]() 分类讨论,分别求出
分类讨论,分别求出![]() 、
、![]() 的解集即可得解;
的解集即可得解;
(2)假设满足条件的![]() 、
、![]() 存在,不妨设
存在,不妨设![]() ,
,![]() 且
且![]() ,由题意得
,由题意得![]() 可得
可得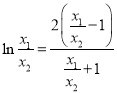 ,令
,令![]() (
(![]() ),构造函数
),构造函数![]() (
(![]() ),求导后证明
),求导后证明![]() 即可得解.
即可得解.
(1)由题可得函数![]() 的定义域为
的定义域为![]() 且
且![]() ,
,
由![]() ,整理得
,整理得![]() .
.
![]() .
.
(ⅰ)当![]() 时,易知
时,易知![]() ,
,![]() ,
,![]() 时
时![]() .
.
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(ⅱ)当![]() 时,令
时,令![]() ,解得
,解得![]() 或
或![]() ,则
,则
①当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 在
在![]() 上递增.
上递增.
②当![]() ,即
,即![]() 时,当
时,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() 单调递减,
单调递减,![]() 单调递增.
单调递增.
③当![]() ,即
,即![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() 单调递减,
单调递减,![]() 单调递增.
单调递增.
综上,当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减.
单调递减.
当![]() 时,
时,![]() 在
在![]() 及
及![]() 上单调递增;
上单调递增;![]() 在
在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() 在
在![]() 上递增.
上递增.
当![]() 时,
时,![]() 在
在![]() 及
及![]() 上单调递增;
上单调递增;![]() 在
在![]() 上递减.
上递减.
(2)满足条件的![]() 、
、![]() 不存在,理由如下:
不存在,理由如下:
假设满足条件的![]() 、
、![]() 存在,不妨设
存在,不妨设![]() ,
,![]() 且
且![]() ,
,
则![]() ,
,
又![]() ,
,
由题可知![]() ,整理可得:
,整理可得: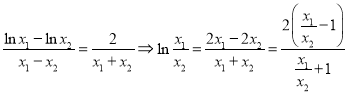 ,
,
令![]() (
(![]() ),构造函数
),构造函数![]() (
(![]() ).
).
则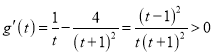 ,
,
所以![]() 在
在![]() 上单调递增,从而
上单调递增,从而![]() ,
,
所以方程![]() 无解,即
无解,即![]() 无解.
无解.
综上,满足条件的A、B不存在.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目