题目内容
设函数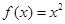 ,
,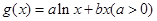 .
.
(Ⅰ)若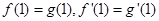 ,求
,求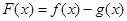 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的结论下,是否存在实常数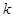 和
和 ,使得
,使得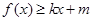 和
和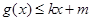 ?若存在,求出
?若存在,求出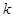 和
和 的值.若不存在,说明理由.
的值.若不存在,说明理由.
(Ⅲ)设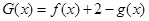 有两个零点
有两个零点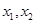 ,且
,且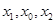 成等差数列,试探究
成等差数列,试探究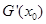 值的符号.
值的符号.
(Ⅰ)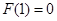 ;(Ⅱ)存在这样的k和m,且
;(Ⅱ)存在这样的k和m,且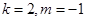 ;(Ⅲ)
;(Ⅲ)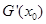 的符号为正.
的符号为正.
解析试题分析:(Ⅰ)首先由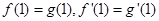 ,得到关于
,得到关于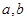 的两个方程,从而求出
的两个方程,从而求出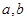 ,这样就可得到
,这样就可得到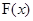 的表达式,根据它的特点可想到用导数的方法求出
的表达式,根据它的特点可想到用导数的方法求出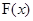 的极小值; (Ⅱ)由(Ⅰ)中所求的
的极小值; (Ⅱ)由(Ⅰ)中所求的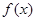 和
和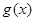 ,易得到它们有一个公共的点
,易得到它们有一个公共的点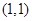 ,且
,且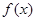 和
和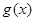 在这个点处有相同的切线
在这个点处有相同的切线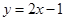 ,这样就可将问题转化为证明
,这样就可将问题转化为证明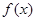 和
和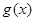 分别在这条切线
分别在这条切线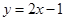 的上方和下方,两线的上下方可转化为函数与0的大小,即证
的上方和下方,两线的上下方可转化为函数与0的大小,即证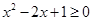 和
和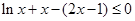 成立,从而得到
成立,从而得到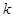 和
和 的值; (Ⅲ)由已知易得
的值; (Ⅲ)由已知易得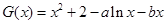 ,由零点的意义,可得到关于
,由零点的意义,可得到关于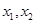 两个方程,根据结构特征将两式相减,得到关于
两个方程,根据结构特征将两式相减,得到关于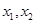 的关系式
的关系式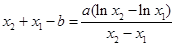 ,又对
,又对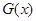 求导,进而得到
求导,进而得到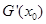 ,结合上面关系可化简得:
,结合上面关系可化简得: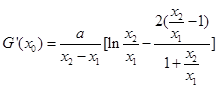 ,针对特征将
,针对特征将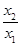 当作一个整体,可转化为关于
当作一个整体,可转化为关于 的函数
的函数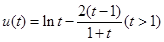 ,对其求导分析得,
,对其求导分析得,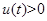 恒成立.
恒成立.
试题解析:解:(Ⅰ)由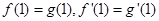 ,得
,得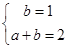 ,解得
,解得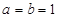 2分
2分
则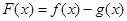 =
=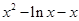 ,
,
利用导数方法可得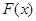 的极小值为
的极小值为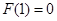 5分
5分
(Ⅱ)因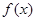 与
与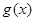 有一个公共点
有一个公共点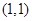 ,而函数
,而函数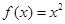 在点
在点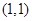 的切线方程为
的切线方程为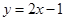 ,
,
下面验证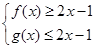 都成立即可 7分
都成立即可 7分
由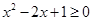 ,得
,得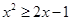 ,知
,知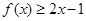 恒成立 8分
恒成立 8分
设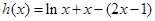 ,即
,即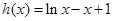 ,易知其在
,易知其在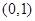 上递增,在
上递增,在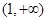 上递减,
上递减,
所以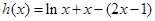 的最大值为
的最大值为 ,所以
,所以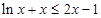 恒成立.
恒成立.
故存在这样的k和m,且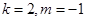 10分
10分
(Ⅲ)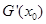 的符号为正. 理由为:因为
的符号为正. 理由为:因为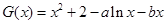 有两个零点
有两个零点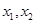 ,则有
,则有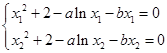 ,两式相减得
,两式相减得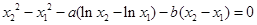 12分
12分
即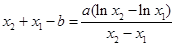 ,于是
,于是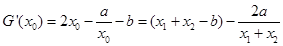
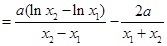
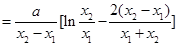
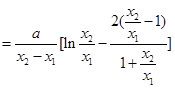 14分
14分
①当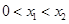 时,令
时,令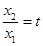 ,则
,则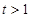 ,且
,且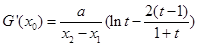 .
.
设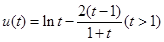 ,则
,则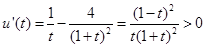 ,则
,则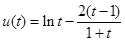 在
在
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
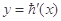 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)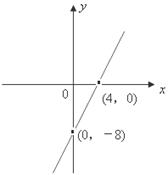
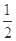 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;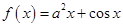 ,
,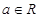 .
. 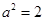 时,求
时,求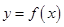 在
在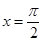 处的切线方程;
处的切线方程; 在
在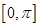 内单调递增,求
内单调递增,求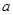 的取值范围.
的取值范围.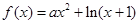 .
.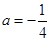 时,求函数
时,求函数 的单调区间;
的单调区间;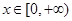 时,不等式
时,不等式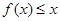 恒成立,求实数
恒成立,求实数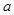 的取值范围.
的取值范围.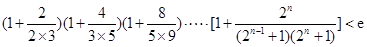 (
(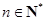 ,e是自然对数的底数).
,e是自然对数的底数).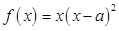 ,
,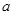 是大于零的常数.
是大于零的常数.  时,求
时,求 的极值;
的极值; 上为单调递增,求实数
上为单调递增,求实数 上存在一点
上存在一点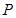 ,使得曲线
,使得曲线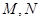 ,且
,且 成立.
成立.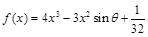 ,其中
,其中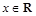 ,
,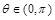 .
.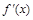 的最小值为
的最小值为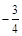 ,试判断函数
,试判断函数 的零点个数,并说明理由;
的零点个数,并说明理由;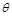 的取值范围.
的取值范围.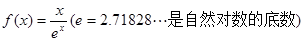 .
.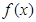 的单调区间及最大值;
的单调区间及最大值;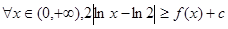 恒成立,试求实数
恒成立,试求实数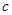 的取值范围.
的取值范围.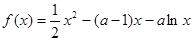 ,
,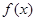 的单调区间;
的单调区间;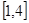 内的最小值为
内的最小值为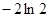 ,求
,求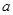 的值.(参考数据
的值.(参考数据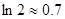 )
) .
.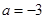 ,
,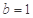 时,求函数
时,求函数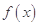 的最大值;
的最大值;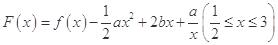 ,其图象上存在一点
,其图象上存在一点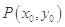 ,使此处切线的斜率
,使此处切线的斜率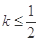 ,求实数
,求实数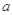 的取值范围;
的取值范围; ,
,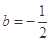 时,方程
时,方程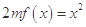 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.