题目内容
(本小题满分12分)
如图,在三棱柱 中,所有的棱长都为2,
中,所有的棱长都为2, .
.
(Ⅰ)求证: ;
;
(Ⅱ)当三棱柱 的体积最大时,求平面
的体积最大时,求平面 与平面
与平面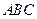 所成的锐角的余弦值.
所成的锐角的余弦值.
如图,在三棱柱
 中,所有的棱长都为2,
中,所有的棱长都为2, .
.(Ⅰ)求证:
 ;
;(Ⅱ)当三棱柱
 的体积最大时,求平面
的体积最大时,求平面 与平面
与平面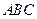 所成的锐角的余弦值.
所成的锐角的余弦值.
(Ⅰ)略(Ⅱ)

(Ⅰ)证明:取 的中点
的中点 ,连接
,连接 ,
,
在三棱柱 中,所有棱长都为2,
中,所有棱长都为2,
则 ,所以
,所以 平面
平面
而 平面
平面 ,故
,故
(Ⅱ)当三棱柱 的体积最大时,点
的体积最大时,点 到平面
到平面 的距离最大,此时
的距离最大,此时 平面
平面 .设平面
.设平面 与平面
与平面 的交线为
的交线为 ,
,
在三棱柱 中,
中, ,
, 平面
平面 ,则
,则
 ,
,
过点 作
作 交于点
交于点 ,连接
,连接 .由
.由 ,
,
 知
知
 平面
平面 ,
,
则

 ,故
,故 为平面
为平面 与平面
与平面 所成二面角的平面角。
所成二面角的平面角。
在 中,
中, ,则
,则
在 中,
中, ,
, ,
,
即平面 与平面
与平面 所成锐角的余弦值为
所成锐角的余弦值为 。
。
方法2:当三棱柱 的体积最大时,点
的体积最大时,点 到平面
到平面 的距离最大,此时
的距离最大,此时 平面
平面 .以
.以 所在的直线分别为
所在的直线分别为 轴,建立直角坐标系,依题意得
轴,建立直角坐标系,依题意得 .
.
由 得
得 ,设平面
,设平面 的一个法向量为
的一个法向量为
而 ,则
,则 ,取
,取
而 平面
平面 ,则平面
,则平面 的一个法向量为
的一个法向量为
于是 ,
,
故平面 与平面
与平面 所成锐角的余弦值为
所成锐角的余弦值为 。
。
 的中点
的中点 ,连接
,连接 ,
,在三棱柱
 中,所有棱长都为2,
中,所有棱长都为2,
则
 ,所以
,所以 平面
平面
而
 平面
平面 ,故
,故
(Ⅱ)当三棱柱
 的体积最大时,点
的体积最大时,点 到平面
到平面 的距离最大,此时
的距离最大,此时 平面
平面 .设平面
.设平面 与平面
与平面 的交线为
的交线为 ,
,在三棱柱
 中,
中, ,
, 平面
平面 ,则
,则
 ,
,过点
 作
作 交于点
交于点 ,连接
,连接 .由
.由 ,
,
 知
知
 平面
平面 ,
,则


 ,故
,故 为平面
为平面 与平面
与平面 所成二面角的平面角。
所成二面角的平面角。在
 中,
中, ,则
,则
在
 中,
中, ,
, ,
,
即平面
 与平面
与平面 所成锐角的余弦值为
所成锐角的余弦值为 。
。方法2:当三棱柱
 的体积最大时,点
的体积最大时,点 到平面
到平面 的距离最大,此时
的距离最大,此时 平面
平面 .以
.以 所在的直线分别为
所在的直线分别为 轴,建立直角坐标系,依题意得
轴,建立直角坐标系,依题意得 .
.由
 得
得 ,设平面
,设平面 的一个法向量为
的一个法向量为
而
 ,则
,则 ,取
,取
而
 平面
平面 ,则平面
,则平面 的一个法向量为
的一个法向量为
于是
 ,
,故平面
 与平面
与平面 所成锐角的余弦值为
所成锐角的余弦值为 。
。
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目




 的六条棱长分别为
的六条棱长分别为 ,且知
,且知 ,则
,则 .
.
 、
、 ;
;  、
、 ;
;  、
、 ;
;  、
、 .
. 中,M、N、G分别是
中,M、N、G分别是 的中点
的中点 与平面
与平面 的位置关系,并证明你的结论
的位置关系,并证明你的结论

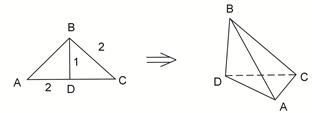
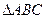 中,
中,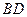 为
为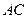 边上高,
边上高,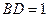 ,
,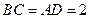 ,沿
,沿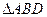 翻折,使得
翻折,使得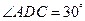 ,得到几何体
,得到几何体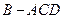 。(1)求证:
。(1)求证: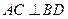 ;
;
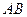 与平面
与平面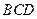 成角的正切值。
成角的正切值。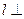 平面
平面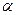 ,直线
,直线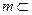 平面
平面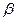 ,给出下列命题中
,给出下列命题中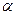 ∥
∥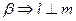 ;②
;②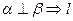 ∥
∥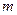 ;
;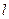 ∥
∥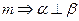 ;④
;④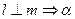 ∥
∥