题目内容
某高校在2013年考试成绩中100名学生的笔试成绩的频率分布直方图如图所示,

(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有 名获得优秀,求
名获得优秀,求 的分布列和数学期望。
的分布列和数学期望。

(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为
 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有 名获得优秀,求
名获得优秀,求 的分布列和数学期望。
的分布列和数学期望。(1)0.3,0.2,0.1
(2) 的分布列如下:
的分布列如下:
 的数学期望
的数学期望
(2)
 的分布列如下:
的分布列如下: | 0 | 1 | 2 | 3 |
 |  |  |  |  |
 的数学期望
的数学期望
试题分析:解:(1)第三组的频率为
 ;第四组的频率为
;第四组的频率为 ;
;第五组的频率为
 3分
3分(2)①设学生甲和学生乙同时进入第二轮面试为事件M:则

所以学生甲和学生乙不同时进入第二轮面试的概率
 7分
7分②由已知得
 ~
~ ,且
,且 ,
, ,
, 的分布列如下:
的分布列如下: | 0 | 1 | 2 | 3 |
 |  |  |  |  |
 的数学期望
的数学期望 13分
13分点评:主要是考查了古典概型概率公式的运用,以及分布列的求解和期望公式,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为 ).
). ,求随机变量
,求随机变量 ,求
,求 为摸出两球中白球的个数,
为摸出两球中白球的个数, 、
、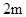 、
、 的钢管各
的钢管各 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根. 时,记事件
时,记事件 {抽取的
{抽取的 根长度相等},求
根长度相等},求 ;
; 时,若用
时,若用 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求 ,
, ,求实数
,求实数 的取值范围.
的取值范围. ,求
,求 ,
, ,
, ~
~ 。若
。若 ,则
,则 的值为
的值为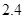



 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
. 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量
