题目内容
设函数
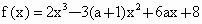 ,其中a∈R,
,其中a∈R,
(1)
若f(x)在x=3处取得极值,求常数a的值;(2)
若f(x)在(-∞,0)上为增函数,求a的取值范围.(2005
·重庆文)
答案:略
解析:
提示:
解析:
|
(1)∵ (2) 令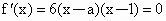 ,得 ,得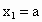 , ,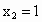 . .
当 a<1时,若x<a或x>1,则,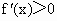 , ,
∴f(x) 在(-∞,a)和(1,+∞)上为增函数.故当 0≤a<1时,f(x)在(-∞,0)上为增函数.当 a≥1时,若x<1或x>a,则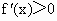 . .
∴f(x) 在(-∞,1)和(a,+∞)上为增函数,从而 f(x)在(-∞,0)上也为增函数.综上所述,当 a∈[0,+∞)时,f(x)在(-∞,0)上为增函数. |
提示:
|
解析:本题所给的函数解析式中只有一个参数 a,第(1)小题只要根据题设条件可直接求出a的值;第(2)小题运用函数的单调性及其在相应区间上函数的导数取值来确定a的取值范围. |

练习册系列答案
相关题目
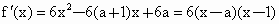 ,又f(x)在x=3处取得极值,∴
,又f(x)在x=3处取得极值,∴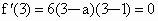 ,解得a=3.将a=3代入原函数式中检验知,当a=3时,x=3为f(x)的极值点.
,解得a=3.将a=3代入原函数式中检验知,当a=3时,x=3为f(x)的极值点. ,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2.如果不等式f(x)>(x-1)lgm在区间[1,+∞)上有解,则实数a的取值范围是 . ,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 . ,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 . ,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)<(x-2)lgm在区间[1,+∞)上恒成立,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)<(x-2)lgm在区间[1,+∞)上恒成立,则实数a的取值范围是 .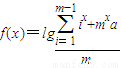 ,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 .
,其中a∈R,m是给定的正整数,且m≥2,如果不等式f(x)>(x-1)lgm在区间[1,+∞)有解,则实数a的取值范围是 .