题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)若函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围;
的取值范围;
(2)若对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)令f(x)=0,变形为![]() ,有两种解题思种,一是换元令
,有两种解题思种,一是换元令![]() ,则
,则![]() ,变形为关于
,变形为关于![]() 的方程
的方程![]() 有正根,分
有正根,分![]() ,
,![]() ,
,![]() 讨论。二是分离参数
讨论。二是分离参数![]() ,只需求右边的值域即可。(2)变形为
,只需求右边的值域即可。(2)变形为![]() ,
,![]() ,恒成立。当
,恒成立。当![]() ,
,![]() ,即
,即![]() ,
,![]() 。
。
试题解析:(1)由函数![]() 有零点得:关于
有零点得:关于![]() 的方程
的方程![]() (
(![]() )有解
)有解
令![]() ,则
,则![]()
于是有,关于![]() 的方程
的方程![]() 有正根
有正根
设![]() ,则函数
,则函数![]() 的图象恒过点
的图象恒过点![]() 且对称轴为
且对称轴为![]()
当![]() 时,
时,![]() 的图象开口向下,故
的图象开口向下,故![]() 恰有一正数解
恰有一正数解
当![]() 时,
时,![]() ,不合题意
,不合题意
当![]() 时,
时,![]() 的图象开口向上,故
的图象开口向上,故![]() 有正数解的条件是
有正数解的条件是![]()
解得:![]()
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.
(2)由“当![]() 时,都有
时,都有![]() ”得:
”得:
![]() ,
,![]() ②
②
∵![]() ,故②变形为:
,故②变形为:![]()
当![]() 时,不等式②简化为
时,不等式②简化为![]() ,此时实数
,此时实数![]()
当![]() 时,有
时,有![]()
∴![]()
∴![]() ,
,![]()
∵当![]() 时,
时,![]() ,
,![]()
![]()
当且仅当![]() 时取等号
时取等号
∴![]()
综上可知,实数![]() 的取值范围
的取值范围![]() .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: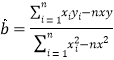 ,
,![]()