题目内容

设x，y满足约束条件
4x-y+4≥0
8x+y-16≤0
x≥0，y≥0
，若目标函数z=ax+by（8b＞a＞0）的最大值为5，则
1
a
+
2
b
的最小值为（　　）
A．5B．6C．7D．8
不等式表示的平面区域如图所示阴影部分，
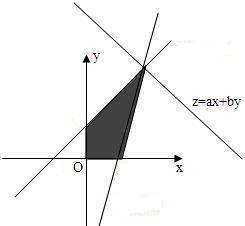
当直线ax+by=z（a＞0，b＞0）过直线4x-y+4=0与直线8x+y-16=0的交点（1，8）时，
目标函数z=ax+by（a＞0，b＞0）取得最大5，
即a+8b=5，
而 (
1
a
+
2
b
)
a+8b
5
=
1
5
[17+
8b
a
+
2a
b
)]≥5≥5．
则
1
a
+
2
b
的最小值为5，
故选A．
练习册系列答案
相关题目
若由不等式组
x≤my+n
x-
3
y≥0
y≥0
，（n＞0）确定的平面区域的边界为三角形，且它的外接圆的圆心在x轴上，则实数m=______．
已知变量x，y满足约束条件
0≤x≤2
0≤y≤1
x+y≥1
，则z=3x+y的最小值为（　　）
A．2B．1C．-1D．-2
若实数x、y满足不等式组
y≥0
x-y≤4
2x-y-2≥0
，则ω=
y-1
x+1
的取值范围是______．
已知实数x，y满足组
x+y≤2
x-y≤0
x≥0
，目标函数z=ax+y仅在点（1，1）处取到最小值，则实数a的取值范围是______．
（理）设x、y满足条件
x-4y≤-3
3x+5y≤25
x≥1
，则2x-y的最大值是______．
设实数x，y满足
x-y-2≤0
x+2y-5≥0
y-2≤0
，则μ=
y
x
的取值范围是（　　）
A．[
1
3
，2]		B．[
1
3
，
1
2
]		C．[
1
2
，2]		D．[2，
5
2
]
画出不等式组
x+2y-1≥0
2x+y-5≤0
y≤x+2
所表示的平面区域并求其面积．
（Ⅰ）在如图的坐标系中作出同时满足约束条件：x+y-1≥0；x-y+1≥0；4x+y-2≥0的可行性区域；
（Ⅱ）若实数x，y满足（Ⅰ）中约束条件，求目标函数
x+y
x
的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网