题目内容
【题目】已知椭圆E： 
+ 
=1（a＞b＞0）的离心率e= 
，并且经过定点P（ 
， 
）． （Ⅰ）求椭圆E的方程；
（Ⅱ）问是否存在直线y=﹣x+m，使直线与椭圆交于A、B两点，满足 
= 
，若存在求m值，若不存在说明理由．
【答案】解（Ⅰ）由题意： 
且 
，又c2=a2﹣b2解得：a2=4，b2=1，即：椭圆E的方程为 
（1）
（Ⅱ）设A（x1 ， y1），B（x2 ， y2）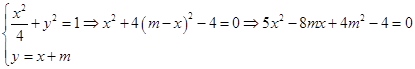
（*）
所以 
= 
由 
，
得 
又方程（*）要有两个不等实根， 
所以m=±2
【解析】（Ⅰ）由已知条件推导出 
且 
，由此能求出椭圆E的方程．（Ⅱ）设A（x1 ， y1），B（x2 ， y2），由 
= 
得，x1x2+y1y2= ，联立方程组利用根与系数的关系求解即可得出m的值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某种产品的质量以其指标值来衡量，其指标值越大表明质量越好，且指标值大于或等于102的产品为优质品，现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测量了每件产品的指标值，得到了下面的试验结果： A配方的频数分布表
指标值分组 | [90，94） | [94，98） | [98，102） | [102，106） | [106，110] |
频数 | 8 | 20 | 42 | 22 | 8 |
B配方的频数分布表
指标值分组 | [90，94） | [94，98） | [98，102） | [102，106） | [106，110] |
频数 | 4 | 12 | 42 | 32 | 10 |
（1）分别估计用A配方，B配方生产的产品的优质品率；
（2）已知用B配方生产的一件产品的利润y（单位：元）与其指标值t的关系式为y= 
，估计用B配方生产的一件产品的利润大于0的概率，并求用B配方生产的上述产品平均每件的利润．
