题目内容
(本题满分14分)如图,有一块边长为1(百米)的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角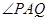 始终为
始终为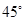 (其中点P,Q分别在边BC,CD上),设
(其中点P,Q分别在边BC,CD上),设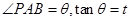 .
.
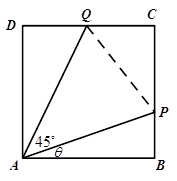

(Ⅰ)用t表示出PQ的长度,并探求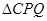 的周长l是否为定值;
的周长l是否为定值;
(Ⅱ)问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少(平方百米)?
 始终为
始终为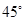 (其中点P,Q分别在边BC,CD上),设
(其中点P,Q分别在边BC,CD上),设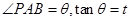 .
.

(Ⅰ)用t表示出PQ的长度,并探求
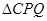 的周长l是否为定值;
的周长l是否为定值;(Ⅱ)问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少(平方百米)?
(1)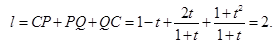 =定值;
=定值;
(2)探照灯照射在正方形 内阴影部分的面积
内阴影部分的面积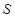 最大为
最大为 平方百米.
平方百米.
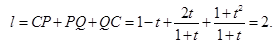 =定值;
=定值;(2)探照灯照射在正方形
 内阴影部分的面积
内阴影部分的面积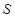 最大为
最大为 平方百米.
平方百米. 试题分析:(1)
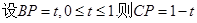 结合三角函数定义得到DQ的值。和勾股定理得到PQ的值,求解周长。
结合三角函数定义得到DQ的值。和勾股定理得到PQ的值,求解周长。(2)根据间接法得到所求解的面积表达式,运用不等式的思想求解得到最值。
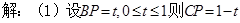
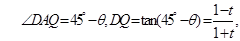 ---2分
---2分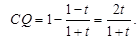 -------------------------------------------------4分
-------------------------------------------------4分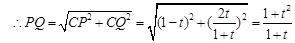 ---------------------6分
---------------------6分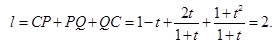 =定值--------------------------------7分
=定值--------------------------------7分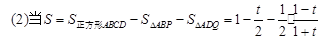 -----------------------10分
-----------------------10分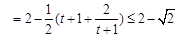 --------------------------------------------------12分
--------------------------------------------------12分 -----------------------------------------13分
-----------------------------------------13分所以探照灯照射在正方形
 内阴影部分的面积
内阴影部分的面积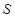 最大为
最大为 平方百米.----14分
平方百米.----14分点评:解决该试题的关键是能合理的设出变量表述各个边长,并能得到其面积的表示,结合均值不等式得到最值。

练习册系列答案
相关题目

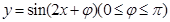 是
是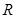 上的偶函数,则
上的偶函数,则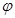 的值是 ( )
的值是 ( )



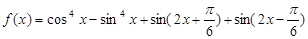
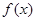 化成
化成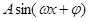 的形式;
的形式;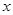 的值;
的值;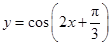 的图像,只需将函数
的图像,只需将函数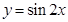 的图像( )
的图像( )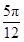 个长度单位
个长度单位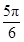 个长度单位
个长度单位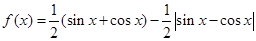 ,则
,则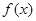 的值域是
的值域是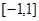
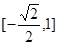
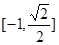
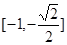
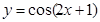 的图象,只要将函数
的图象,只要将函数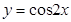 的图象( ).
的图象( ).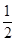 个单位
个单位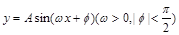 的图象向左平移
的图象向左平移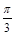 个单位得到
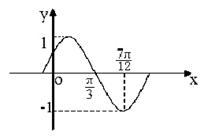
个单位得到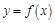 的图象(如图),则
的图象(如图),则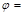 ( )
( )
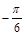
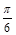
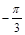
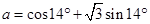 ,
,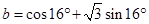 ,
,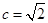 ,则
,则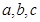 的大小关系是( )
的大小关系是( )


