题目内容
若f（x），g（x）满足f′（x）=g′（x），则f（x）与g（x）满足（ ）
| A．f（x）=g（x） | B．f（x）-g（x）为常数 |
| C．f（x）=g（x）=0 | D．f（x）+g（x）为常数 |
由f′（x）=g′（x），得f′（x）-g′（x）=0，
即[f（x）-g（x）]′=0，所以f（x）-g（x）=C（C为常数）．
故选B．
即[f（x）-g（x）]′=0，所以f（x）-g（x）=C（C为常数）．
故选B．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
的函数
，其导函数为
．记函数
在区间
上的最大值为
．
在
处有极值
，试确定
的值；
，证明对任意的
，都有
；
对任意的
的最大值．
上任何一点
的切线与两坐标轴围成三角形面积是一个常数。
米的距离，其中a为常数且
，自第一辆车车头进入隧道至第55辆车车尾离开隧道所用时间为y(秒) ． （1）将y表示为x的函数；（2）求车队通过隧道所用时间取最小值时车队的速度．
，直线
与函数
的图象都相切于点
． 
的解析式；
（其中
是
的导函数），求函数
的值域．
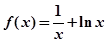的极小值为 ；
，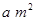