题目内容
【题目】已知点M是圆心为E的圆![]() 上的动点,点
上的动点,点![]() ,线段MF的垂直平分线交EM于点P.
,线段MF的垂直平分线交EM于点P.
(Ⅰ)求动点P的轨迹C的方程;
(Ⅱ)过原点O作直线交(Ⅰ)中轨迹C于点A、B,点D满足![]() ,试求四边形AFBD的面积的取值范围.
,试求四边形AFBD的面积的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)利用椭圆定义求出点P的轨迹是椭圆,其中![]() ,
, ![]() ,求出椭圆方程即可;
,求出椭圆方程即可;
(Ⅱ)求出SAFBD=2S△AFB,通过讨论AB是短轴、AB是长轴的情况,求出四边形的面积即可.
试题解析:
(Ⅰ)∵点P为线段MF的垂直平分线,
∴![]()
∴![]()
所以点P的轨迹为椭圆,其中![]() ,
, ![]()
所以点P的轨迹C的方程为![]()
(Ⅱ)由![]() ,知四边形AFBD为平行四边形
,知四边形AFBD为平行四边形
所以![]()
① 当AB为短轴时, ![]()
即![]()
② 当AB为长轴时,易知四边形AFBD不是平行四边形,所以AB的斜率不为0.
③ 当直线AB的斜率存在且不为0时,设AB的方程为![]()
联立方程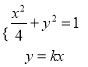 消去x,整理得
消去x,整理得![]()
则![]() ,
, ![]()
![]() ,
,
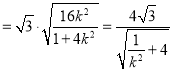 ,
,
而![]() ,所以
,所以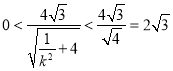
综上,四边形AFBD的面积的取值范围为![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





