题目内容
抛物线x=8y2的焦点坐标为 .

解析试题分析:首先把抛物线化为标准方程 ,由
,由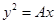 形式焦点坐标为
形式焦点坐标为 可得
可得 .
.
考点:求抛物线焦点坐标.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
题目内容
抛物线x=8y2的焦点坐标为 .

解析试题分析:首先把抛物线化为标准方程 ,由
,由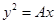 形式焦点坐标为
形式焦点坐标为 可得
可得 .
.
考点:求抛物线焦点坐标.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案