题目内容
7. 如图,在矩形ABCD中,AB=4,BC=3,沿对角线AC把矩形折成二面角D-AC-B,并且D点在平面ABC内的射影落在AB上.
如图,在矩形ABCD中,AB=4,BC=3,沿对角线AC把矩形折成二面角D-AC-B,并且D点在平面ABC内的射影落在AB上.(1)证明:AD⊥平面DBC;
(2)求三棱锥D-ABC的体积;
(3)若在四面体D-ABC内有一球,当球的体积最大时,球的半径是多少?
分析 (1)首先由D点在平面ABC内的射影落在AB上.得到面面垂直,结合翻折中不变的直角,转换出BC与平面ABD垂直,进而得到AD与平面BCD垂直;
(2)求三棱锥体积首先找到底面积和高分别为多少,底面为直角三角形,高为D到AB边的距离;
(3)三棱锥内体积最大的球为内切球,求解球的半径时采用将三棱锥体积分割的方法计算,分割成的每一个小三棱锥的底面为原棱锥的四个表面,高为内切球的半径.
解答  (1)证明:因为D点在平面ABC内的射影落在AB上,所以平面ABC⊥平面ABD,
(1)证明:因为D点在平面ABC内的射影落在AB上,所以平面ABC⊥平面ABD,
因为BC⊥AB,平面ABC∩平面ABD=AB,
所以BC⊥平面ABD,
所以BC⊥AD,
因为AD⊥CD,BC∩CD=C,
所以AD⊥平面DBC;
(2)解:作DH垂直于底面交AB于点H,
因为AD⊥平面DBC,所以AD⊥平面DB,
因为AD=BC=3,AB=4,所以BD=$\sqrt{16-9}$=$\sqrt{7}$
利用面积相等AD×BD=AB×DH,所以DH=$\frac{3\sqrt{7}}{4}$.
所以三棱锥D-ABC的体积V=$\frac{1}{3}{S}_{△ABC}•DH$=$\frac{1}{3}×6×\frac{3\sqrt{7}}{4}$=$\frac{3\sqrt{7}}{2}$.
(3)解:当球的体积最大时,球与三棱锥D-ABC各面都相切,设球的半径为R,球心为O,则有
VD-ABC=VO-ABC+VO-BCD+VO-ACD+VO-ABD=$\frac{1}{3}R$(S△ABC+S△BCD+S△ACD+S△ABD)
S△ABC=S△ACD=6,S△ABD=S△BCD=$\frac{1}{2}•3•\sqrt{7}$=$\frac{3\sqrt{7}}{2}$,
所以$\frac{1}{3}R$(6+6+$\frac{3\sqrt{7}}{2}$+$\frac{3\sqrt{7}}{2}$)=$\frac{3\sqrt{7}}{2}$,
所以R=$\frac{4\sqrt{7}-7}{6}$.
点评 本题考查线面垂直的判定,三棱锥D-ABC的体积,考查分割法的运用,考查学生分析解决问题的能力,属于中档题.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案| A. | $\frac{4}{3}π$ | B. | $\frac{2}{3}π$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
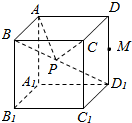 在棱长为1的正方体ABCD-A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$.
在棱长为1的正方体ABCD-A1B1C1D1中,点P是它的体对角线BD1上一动点,则|AP|+|PC|的最小值是$\frac{2\sqrt{6}}{3}$.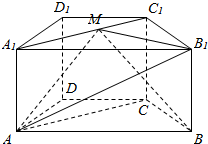 在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.
在四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB∥CD,AD=DC=CB=1,∠ABC=$\frac{π}{3}$,对角面A1ACC1为矩形,平面A1ACC1⊥平面ABCD,CC1=1.