题目内容
如图所示,将一矩形花坛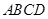 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛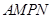 ,要求
,要求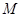 在
在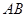 的延长线上,
的延长线上,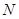 在
在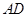 的延长线上,且对角线
的延长线上,且对角线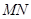 过
过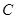 点.已知
点.已知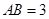 米,
米,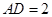 米。
米。
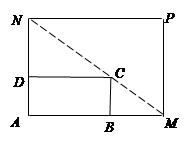
(1)设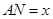 (单位:米),要使花坛
(单位:米),要使花坛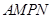 的面积大于32平方米,求
的面积大于32平方米,求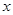 的取值范围;
的取值范围;
(2)若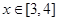 (单位:米),则当
(单位:米),则当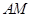 ,
,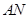 的长度分别是多少时,花坛
的长度分别是多少时,花坛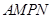 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
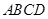 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛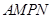 ,要求
,要求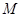 在
在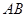 的延长线上,
的延长线上,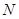 在
在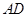 的延长线上,且对角线
的延长线上,且对角线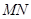 过
过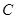 点.已知
点.已知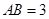 米,
米,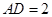 米。
米。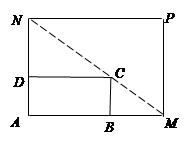
(1)设
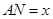 (单位:米),要使花坛
(单位:米),要使花坛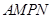 的面积大于32平方米,求
的面积大于32平方米,求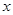 的取值范围;
的取值范围; (2)若
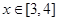 (单位:米),则当
(单位:米),则当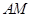 ,
,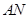 的长度分别是多少时,花坛
的长度分别是多少时,花坛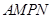 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.(Ⅰ) ;(Ⅱ)花坛
;(Ⅱ)花坛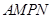 的面积最大27平方米,此时
的面积最大27平方米,此时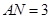 米,
米,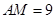 米 .
米 .
 ;(Ⅱ)花坛
;(Ⅱ)花坛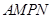 的面积最大27平方米,此时
的面积最大27平方米,此时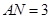 米,
米,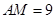 米 .
米 .试题分析:(Ⅰ)把
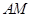 用
用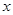 表示后,再把矩形
表示后,再把矩形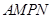 面积表示出来,解不等式可得;(Ⅱ)对(Ⅰ)中的函数解析式,以导数为工具,求出最大值.
面积表示出来,解不等式可得;(Ⅱ)对(Ⅰ)中的函数解析式,以导数为工具,求出最大值.试题解析:由于
 即
即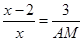 ,则
,则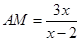
故
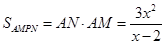 4分
4分(1)由
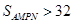 得
得 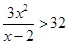 ,
,因为
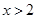 ,所以
,所以 ,即
,即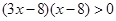
从而
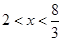 或
或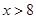
即
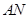 长的取值范围是
长的取值范围是 8分
8分(2)令
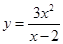 ,则
,则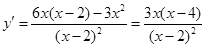 11分
11分因为当
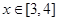 时,
时,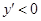 ,所以函数
,所以函数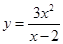 在
在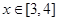 上为单调递减函数,
上为单调递减函数,从而当
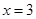 时
时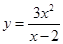 取得最大值,即花坛
取得最大值,即花坛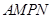 的面积最大27平方米,
的面积最大27平方米,此时
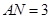 米,
米,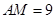 米 16分
米 16分
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
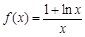 .
.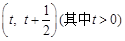 上存在极值,求实数
上存在极值,求实数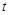 的取值范围;
的取值范围;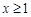 时,不等式
时,不等式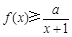 恒成立,求实数
恒成立,求实数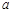 的取值范围.
的取值范围.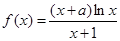 ,曲线
,曲线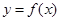 在点
在点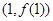 处的切线与直线
处的切线与直线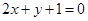 垂直.
垂直.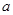 的值;
的值;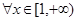 ,
,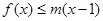 恒成立,求
恒成立,求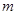 的范围.
的范围.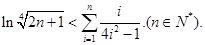
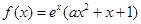 (
(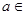 R),且该函数曲线
R),且该函数曲线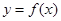 在
在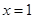 处的切线与
处的切线与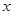 轴平行.
轴平行.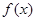 的单调性;
的单调性;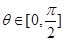 时,
时,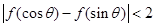 .
.


 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,当
,当 时,有
时,有 恒成立,则不等式
恒成立,则不等式 的解集是( )
的解集是( )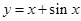 在点
在点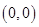 处的切线方程是 .
处的切线方程是 .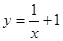 在点(1,2)处的切线与直线
在点(1,2)处的切线与直线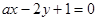 平行,则
平行,则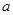 =( )
=( ) 的单调递减区间是
的单调递减区间是