题目内容
已知函数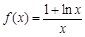 .
.
(Ⅰ)若函数在区间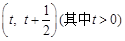 上存在极值,求实数
上存在极值,求实数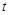 的取值范围;
的取值范围;
(Ⅱ)如果当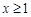 时,不等式
时,不等式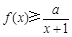 恒成立,求实数
恒成立,求实数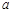 的取值范围.
的取值范围.
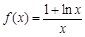 .
.(Ⅰ)若函数在区间
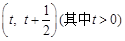 上存在极值,求实数
上存在极值,求实数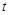 的取值范围;
的取值范围;(Ⅱ)如果当
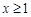 时,不等式
时,不等式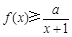 恒成立,求实数
恒成立,求实数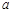 的取值范围.
的取值范围.(Ⅰ)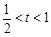 ;(Ⅱ)
;(Ⅱ)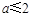 .
.
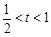 ;(Ⅱ)
;(Ⅱ)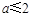 .
.试题分析:(Ⅰ)先对函数求导,求出函数的极值,根据函数
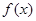 在区间
在区间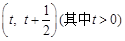 上存在极值,
上存在极值,所以
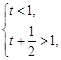 从而解得
从而解得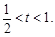 (Ⅱ)不等式
(Ⅱ)不等式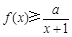 恒成立问题转化为求函数的最值问题.
恒成立问题转化为求函数的最值问题.试题解析:
解:(Ⅰ)因为
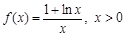 ,则
,则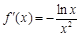 , (2分)
, (2分)当
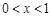 时,
时,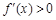 ;当
;当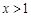 时,
时,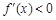 .
.所以
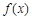 在
在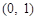 上单调递增;在
上单调递增;在 上单调递减,
上单调递减,所以函数
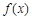 在
在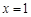 处取得极大值. (4分)
处取得极大值. (4分)因为函数
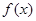 在区间
在区间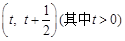 上存在极值,
上存在极值,所以
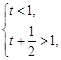 解得
解得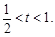 (6分)
(6分)(Ⅱ)不等式
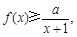 即为
即为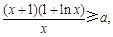 记
记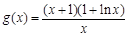 ,
,所以
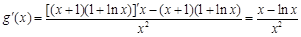 , (9分)
, (9分)令
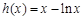 ,则
,则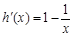 ,
, ,
,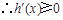 ,
, 在
在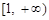 上单调递增,
上单调递增,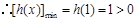 ,从而
,从而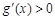 ,
,故
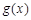 在
在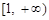 上也单调递增,所以
上也单调递增,所以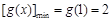 ,
,所以
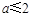 . (12分)
. (12分)
练习册系列答案
相关题目
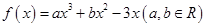 在点
在点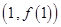 处的切线方程为
处的切线方程为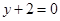 .
.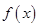 的解析式;
的解析式;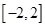 上任意两个自变量的值
上任意两个自变量的值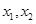 都有
都有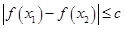 ,求实数
,求实数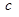 的最小值;
的最小值;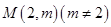 可作曲线
可作曲线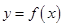 的三条切线,求实数
的三条切线,求实数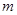 的取值范围.
的取值范围. ,
, .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上是减函数,求
上是减函数,求 的取值范围.
的取值范围.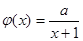 ,
,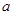 为正常数.
为正常数.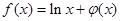 ,且
,且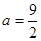 ,求函数
,求函数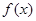 的单调增区间;
的单调增区间;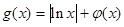 ,且对任意
,且对任意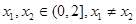 都有
都有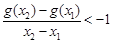 ,求
,求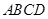 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛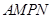 ,要求
,要求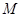 在
在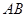 的延长线上,
的延长线上,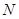 在
在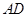 的延长线上,且对角线
的延长线上,且对角线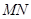 过
过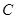 点.已知
点.已知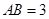 米,
米,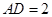 米。
米。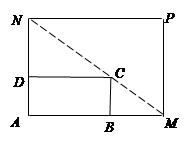
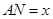 (单位:米),要使花坛
(单位:米),要使花坛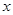 的取值范围;
的取值范围; 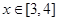 (单位:米),则当
(单位:米),则当 ,
, 的长度分别是多少时,花坛
的长度分别是多少时,花坛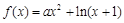 .
.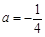 时,求函数
时,求函数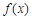 的单调区间;
的单调区间;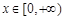 时,不等式
时,不等式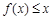 恒成立,求实数
恒成立,求实数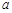 的取值范围.
的取值范围.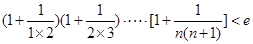 (
(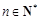 ,e是自然对数的底数).
,e是自然对数的底数).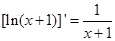
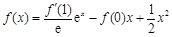 在点
在点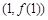 处的切线方程为_________.
处的切线方程为_________. 在点
在点 处的切线与
处的切线与 轴的交点横坐标为
轴的交点横坐标为 ,则
,则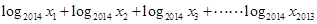 的值为( )
的值为( )



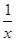 )’=1+
)’=1+