题目内容
已知双曲线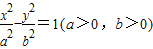 的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为
的右焦点为F,右准线与一条渐近线交于点A,△OAF的面积为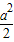 (O为原点),则两条渐近线的夹角为 .
(O为原点),则两条渐近线的夹角为 .
【答案】分析:设A点是斜率为正的渐近线与右准线的交点,进而根据双曲线方程求得渐近线方程和右准线方程,进而把这两个方程联立求得点A的坐标,△OAF的面积以OF为底边计算的话,其上的高就是A点的纵坐标的绝对值,即: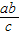 ,进而表示出△OAF的面积建立等式求得a=b,进而可知双曲线渐近线的斜率,可知其垂直,进而可推出答案.
,进而表示出△OAF的面积建立等式求得a=b,进而可知双曲线渐近线的斜率,可知其垂直,进而可推出答案.
解答:解:设A点是斜率为正的渐近线与右准线的交点
双曲线斜率为正的渐近线方程为:y=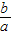 x
x
而右准线为:x=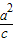
于是,渐近线与右准线的交点A,其横坐标就是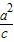 ,纵坐标可求出是:
,纵坐标可求出是:
y=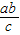
△OAF的面积若是以OF为底边计算的话,其上的高就是A点的纵坐标的绝对值,即: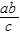
∴S△OAF=|OF|•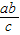 •
• =
=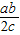 =
=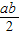
由题意有: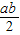 =
=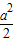
∴a=b
∴双曲线两条渐近线就是:y=±x
∴两条渐近线相互垂直
∴它们的夹角很容易得出是90°
故答案为90°
点评:本题主要考查了双曲线的简单性质.从近三年高考情况看,圆锥曲线的定义、方程和性质仍是高考考查的重点内容,平时应注意多积累.
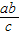 ,进而表示出△OAF的面积建立等式求得a=b,进而可知双曲线渐近线的斜率,可知其垂直,进而可推出答案.
,进而表示出△OAF的面积建立等式求得a=b,进而可知双曲线渐近线的斜率,可知其垂直,进而可推出答案.解答:解:设A点是斜率为正的渐近线与右准线的交点
双曲线斜率为正的渐近线方程为:y=
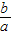 x
x而右准线为:x=
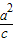
于是,渐近线与右准线的交点A,其横坐标就是
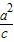 ,纵坐标可求出是:
,纵坐标可求出是:y=
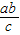
△OAF的面积若是以OF为底边计算的话,其上的高就是A点的纵坐标的绝对值,即:
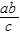
∴S△OAF=|OF|•
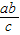 •
• =
=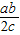 =
=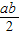
由题意有:
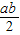 =
=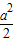
∴a=b
∴双曲线两条渐近线就是:y=±x
∴两条渐近线相互垂直
∴它们的夹角很容易得出是90°
故答案为90°
点评:本题主要考查了双曲线的简单性质.从近三年高考情况看,圆锥曲线的定义、方程和性质仍是高考考查的重点内容,平时应注意多积累.

练习册系列答案
相关题目