题目内容
15.求值(1)$sin(-\frac{35π}{4})$
(2)$\frac{{cos(-{{585}°})}}{{tan{{495}°}+sin(-{{690}°})}}$.
分析 直接利用诱导公式化简通过特殊角的三角函数求值即可.
解答 解:(1)$sin(-\frac{35π}{4})$=-sin$\frac{3π}{4}$=-$\frac{\sqrt{2}}{2}$.
(2)$\frac{{cos(-{{585}°})}}{{tan{{495}°}+sin(-{{690}°})}}$=$\frac{-cos45°}{-tan45°+sin30°}$=$\frac{-\frac{\sqrt{2}}{2}}{-1+\frac{1}{2}}$=$\sqrt{2}$.
点评 本题考查诱导公式的应用,特殊角的三角函数值的求法,考查计算能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
3.下表是某食堂热饮小卖场连续5天内卖出热饮的杯数与当天气温的对比表:
若热饮杯数y与气温x近似地满足线性关系,则其关系式最接近的是( )
| 气温/(℃) | 4 | 2 | 1 | -1 | -3 |
| 杯数 | 24 | 36 | 40 | 49 | 61 |
| A. | y=4x+36 | B. | y=5x+20 | C. | y=-4x+44 | D. | y=-5x+45 |
20.sin165°•sin75°+sin105°•sin15°的值是( )
| A. | 0 | B. | -$\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
4.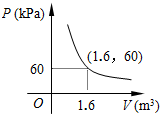 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$m3 | B. | 小于$\frac{5}{4}$m3 | C. | 不小于$\frac{4}{5}$m3 | D. | 不大于$\frac{4}{5}$m3 |
5.集合M={x|log2(x2-3x+2)<1},N={x|x<a},若M⊆N,则a的取值范围是( )
| A. | [3,+∞) | B. | (3,+∞) | C. | [1,+∞) | D. | (1,+∞) |