题目内容
6.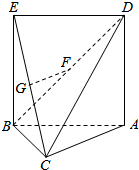 如图,四棱锥C-ABED中,AC=4,BC=3,四边形ABED是边长为$\sqrt{13}$的正方形,若G,F分别是线段EC,BD的中点.
如图,四棱锥C-ABED中,AC=4,BC=3,四边形ABED是边长为$\sqrt{13}$的正方形,若G,F分别是线段EC,BD的中点.(1)求证:GF∥底面ABC;
(2)若点P为线段CD的中点,求三角形GFP的面积.
分析 (1)证明GF平行于平面ABC内的一条直线AC即可;
(2)利用中位线定理,求出△PFG的三边长,再由余弦定理求出其中一角,即可求三角形的面积.
解答  解:(1)证明:如图所示,连接AE,
解:(1)证明:如图所示,连接AE,
由题意知,F为AE中点,
GF为△AEC的中位线,
∴GF∥AC;
又∵AC?平面ABC,
∴GF∥平面ABC;
(2)连接PG,PF
由(1)知:GF=$\frac{1}{2}$AC=2,
同理可得:PF=$\frac{1}{2}$BC=$\frac{3}{2}$,
PG=$\frac{1}{2}$DE=$\frac{\sqrt{13}}{2}$;
∴cos∠PFG=$\frac{{PF}^{2}{+GF}^{2}{-PG}^{2}}{2PF•GF}$=$\frac{1}{2}$,
∴∠PFG=$\frac{π}{3}$;
∴S△PFG=$\frac{1}{2}$PF•GF•sin∠PFG
=$\frac{1}{2}$×$\frac{3}{2}$×2×$\frac{\sqrt{3}}{2}$
=$\frac{3\sqrt{3}}{4}$.
点评 本题考查了直线与平面平行的判断问题,也考查了正弦、余弦定理的应用问题,是综合性题目.

练习册系列答案
相关题目
16.已知椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于下表中:
(1)求椭圆C1和抛物线C2的标准方程.
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点,试证:直线PA,PF,PB的斜率成等差数列.
| x | -$\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点,试证:直线PA,PF,PB的斜率成等差数列.
17.“五一”期间,三个家庭(每家均为一对夫妇和一个孩子)去“抚顺三块石国家森林公园”游玩,在某一景区前合影留念,要求前排站三个小孩,后排为三对夫妇,则每队夫妇均相邻,且小孩恰与自家父母排列的顺序一致的概率( )
| A. | $\frac{1}{15}$ | B. | $\frac{1}{90}$ | C. | $\frac{1}{180}$ | D. | $\frac{1}{360}$ |
14.已知$\overrightarrow{e}$和$\overrightarrow{f}$是互相垂直的单位向量,向量$\overrightarrow{{a}_{n}}$满足:$\overrightarrow{e}•\overrightarrow{{a}_{n}}$=n,$\overrightarrow{f}•\overrightarrow{{a}_{n}}$=2n,n∈N*.设θn为$\overrightarrow{{a}_{n+1}}$-$\overrightarrow{{a}_{n}}$和$\overrightarrow{{a}_{n+2}}$-$\overrightarrow{{a}_{n+1}}$的夹角,则( )
| A. | On随着n的增大而增大 | B. | On随着n的增大而减小 | ||
| C. | 随着n的增大,On先增大后减小 | D. | 随着n的增大,On先减小后增大 |
1.在△ABC 中,三个角A、B、C成等差数列,则角B等于( )
| A. | 30° | B. | 60° | C. | 90° | D. | 不能确定 |
15.能化为普通方程x2+y-1=0的参数方程是( )
| A. | $\left\{\begin{array}{l}x=sint\\ y={cos^2}t\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=tanφ\\ y=1-{tan^2}φ\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=\sqrt{1-t}\\ y=t\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=cosθ}\\{y=si{n}^{2}θ}\end{array}\right.$ |