题目内容
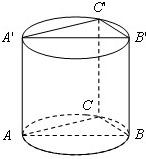 如图,直三棱柱ABC-A′B′C′内接于高为
如图,直三棱柱ABC-A′B′C′内接于高为| 2 |
| 2 |
求(1)圆柱的全面积;
(2)异面直线AB′与CO所成的角的大小;
(3)求二面角A′-BC-A的大小.
分析:(1)先由等腰直角三角形的特征求得圆柱底面半径,再利用圆柱侧面积公式和底面积公式求解.
(2)通过圆柱的结构特征可知co⊥平面ABB′A′,从而有co⊥AB′,得到∠COO′=90°,从而得到结论.
(3)由CB⊥平面A′AC,易得BC⊥CA′,可知∠A′CA是二面角的平面角,用正切函数可求得结论.
(2)通过圆柱的结构特征可知co⊥平面ABB′A′,从而有co⊥AB′,得到∠COO′=90°,从而得到结论.
(3)由CB⊥平面A′AC,易得BC⊥CA′,可知∠A′CA是二面角的平面角,用正切函数可求得结论.
解答: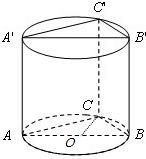 解:(1)根据题意:底面半径为:r=
解:(1)根据题意:底面半径为:r=
,
∴S=2πr2+2πrh=3π;
(2)∵co⊥平面ABB′A′
∴co⊥AB′
∴∠COO′=90°
∴异面直线AB′与CO所成的角是90°
(3)∵CB⊥平面A′AC,
∴BC⊥CA′,
∴∠A′CA是二面角的平面角
∴A′CA=arctan
 解:(1)根据题意:底面半径为:r=
解:(1)根据题意:底面半径为:r=
| ||
| 2 |
∴S=2πr2+2πrh=3π;
(2)∵co⊥平面ABB′A′
∴co⊥AB′
∴∠COO′=90°
∴异面直线AB′与CO所成的角是90°
(3)∵CB⊥平面A′AC,
∴BC⊥CA′,
∴∠A′CA是二面角的平面角
∴A′CA=arctan
| 2 |
点评:本题主要考查圆柱的几何特征,异面直线所成的角及二面角问题,同时,还考查了转化思想和学生的运算能力,属中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.