题目内容
圆柱内有一个三棱柱,三棱柱的底面三角形是圆柱底面圆的内接三角形,并且三棱柱底面是正三角形,如果圆柱的体积是16π,底面直径与母线长相等,那么三棱柱的体积为 .
分析:设圆柱的底面圆的半径为r,其内接正三角形的边长为a,由圆柱的体积求出r,根据正弦定理求出a,代入棱柱的体积公式计算.
解答:解:设圆柱的底面圆的半径为r,其内接正三角形的边长为a,
由圆柱的体积是16π,
则π×r2×2r=16π,
∴r=2,
∵
=2r=4,
∴a=2
,
∴三棱柱的体积V=
×2
×2
×
×4=12
.
故答案是:12
.
由圆柱的体积是16π,
则π×r2×2r=16π,
∴r=2,
∵
| a |
| sin60° |
∴a=2
| 3 |
∴三棱柱的体积V=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
故答案是:12
| 3 |
点评:本题借助接体考查了圆柱与棱柱的体积计算,解答的关键是由圆的半径求出其内接正三角形的边长.

练习册系列答案
相关题目
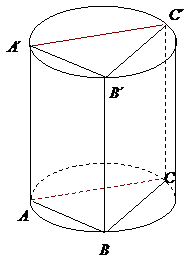
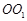 内有一个三棱柱
内有一个三棱柱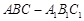 ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.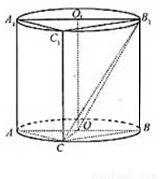
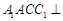 平面
平面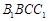 ;
;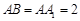 ,在圆柱
,在圆柱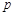 .
.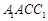 与平面
与平面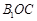 所成的角为
所成的角为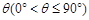 ,当
,当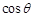 的值.
的值. 内有一个三棱柱
内有一个三棱柱 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且 是圆
是圆 的直径.
的直径.
 的体积;
的体积; ⊥平面
⊥平面
